
【题目】将一副三角板中的两块直角三角尺的直角顶点O按如图方式叠放在一起.
(1)如图(1)若∠BOD=35°,则∠AOC= .
如图(2)若∠BOD=35°,则∠AOC= .
(2)猜想∠AOC与∠BOD的数量关系,并结合图(1)说明理由.
(3)三角尺AOB不动,将三角尺COD的OD边与OA边重合,然后绕点O按顺时针或逆时针方向任意转动一个角度,当∠AOD(0°<∠AOD<90°)等于多少度时,这两块三角尺各有一条边互相垂直.(填空)
(3) 当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .
当 ⊥ 时,∠AOD = .

【答案】(1)145,145;(2)详见解析;(3)详见解析.
【解析】
(1)由于是两直角三角形板重叠,根据∠AOC=∠AOB+∠COD-∠BOD可计算出∠AOC的度数;根据∠AOC=360°-∠BOD-∠AOB-∠COD可计算出∠AOC的度数;(2)由∠AOD+∠BOD+∠BOD+∠BOC=180°且∠AOD+∠BOD+∠BOC=∠AOC可知两角互补;(3)分别利用OD⊥AB、CD⊥OB、CD⊥AB、OC⊥AB分别求出即可.
解:(1)若∠BOD=35°,
∵∠AOB=∠COD=90°,
∴∠AOC=∠AOB+∠COD-∠BOD=90°+90°-35°=145°;
如图2,若∠BOD=35°,
则∠AOC=360°-∠BOD-∠AOB-∠COD
=360°-35°-90°-90°
=145°;
(2)∠AOC与∠BOD互补.
∵∠AOB=∠COD=90°,
∴∠AOD+∠BOD+∠BOD+∠BOC=180°.
∵∠AOD+∠BOD+∠BOC=∠AOC,
∴∠AOC+∠BOD=180°,
即∠AOC与∠BOD互补.
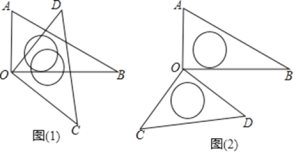
(3) 当 AB ⊥ OD 时,∠AOD = 30° .
当 CD ⊥ OA 时,∠AOD = 45° .
当 OC ⊥ AB 时,∠AOD = 60° .
当 AB ⊥ CD 时,∠AOD = 75° .
即∠AOD角度所有可能的值为:30°、45°、60°、75°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某汽车制造厂开发一款新式电动汽车,计划一年生产安装![]() 辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:
辆.由于抽调不出足够的熟练工来完成新式电动汽车的安装,工厂决定招聘一些新工人.他们经过培训后上岗,也能独立进行电动汽车的安装.生产开始后,调研部门发现:![]() 名熟练工和
名熟练工和![]() 名新工人每月可安装
名新工人每月可安装![]() 辆电动汽车;
辆电动汽车;![]() 名熟练工和
名熟练工和![]() 名新工人每月可安装
名新工人每月可安装![]() 辆电动汽车.
辆电动汽车.
(1)每名熟练工和新工人每月分别可以安装多少辆电动汽车?
(2)如果工厂招聘![]() 名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
名新工人,使得招聘的新工人和抽调的熟练工刚好能完成一年的安装任务,那么工厂有哪几种新工人的招聘方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,A(1,2),B(3,1),C(﹣2,﹣1).

(1)在图中作出△ABC关于x轴的对称图形△A1B1C1 ;
(2)写出点A1 , B1 , C1的坐标(直接写答案), A1________ ,B1________ ,C1________;
(3)求△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1,L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.
(1)如图2,已知抛物线L3:y=2x2-8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;
(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;
(3)若抛物y=a1 (x-m) 2+n的任意一条友好抛物线的解析式为y=a2 (x-h) 2+k,请写出a1与a2的关系式,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=70°,将△ABC绕点A逆时针旋转,得到△AB'C',连接C'C.若C'C∥AB,则∠BAB'=______°.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直线y=m是平行于X轴的直线,将抛物线y=-![]() x2-4x在直线y=m上侧的部分沿直线 y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图像,若新的函数图像刚好与 直线y=-x有3个交点,则满足条件的m 的值为_________
x2-4x在直线y=m上侧的部分沿直线 y=m翻折,翻折后的部分与没有翻折的部分组成新的函数图像,若新的函数图像刚好与 直线y=-x有3个交点,则满足条件的m 的值为_________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列推理过程,在括号中填写理由.
如图,E点为DF上的点,B为AC上的点,∠1=∠2,∠C=∠D.试说明:AC∥DF.
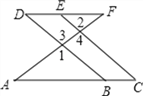
解:∵∠1=∠2(已知),∠1=∠3(______________),
∴∠2=∠3(___________________).
∴__∥__(__________________________________).
∴∠C=∠ABD (________________________________).
又∵∠C=∠D(____________),
∴∠D=∠ABD(等量代换)
∴AC∥DF(______________________________).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,将BC沿BD所在的直线折叠,使点C落在AB边上的E点处.
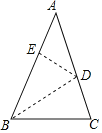
(1)若∠ADE=30°,求∠BDC的度数.
(2)若AB=AC=8,BC=5,求三角形AED的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,连接BD,且BD=CD,过点A作AM⊥BD于点M,过点D作DN⊥AB于点N,且DN=4,在DB的延长线上取一点P,满足∠ABD=∠MAP+∠PAB,则AP=______.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com