
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B��C������ֱ�Ϊ��1��0������0��1��������1��0����һ���綯��ߴ�����ԭ��O��������һ����Ծ����P1��ʹ�õ�P1���O���ڵ�A�����ĶԳƣ��ڶ�����Ծ����P2��ʹ�õ�P2���P1���ڵ�B�����ĶԳƣ���������Ծ����P3��ʹ�õ�P3���P2���ڵ�C�����ĶԳƣ����Ĵ���Ծ����P4��ʹ�õ�P4���P3���ڵ�A�����ĶԳƣ��������Ծ����P5��ʹ�õ�P5���P4���ڵ�B�����ĶԳƣ����մ˹����ظ���ȥ�����![]() ������Ϊ_______��
������Ϊ_______��

���𰸡���2��2��
��������
�������ĶԳƵ������ҳ�����Pn�����꣬��������ı仯�ҳ��仯������P6n��0��0����P6n+1��2��0����P6n+2��-2��2����P6n+3��0��-2����P6n+4��2��2����P6n+5��-2��0����nΪ��Ȼ�����������˹��ɼ��ɵó����ۣ�
�۲죬���ֹ��ɣ�P0��0��0����P1��2��0����P2��-2��2����P3��0��-2����P4��2��2����P5��-2��0����P6��0��0����P7��2��0��������
��P6n��0��0����P6n+1��2��0����P6n+2��-2��2����P6n+3��0��-2����P6n+4��2��2����P6n+5��-2��0����nΪ��Ȼ������
��2020=6��336+4��
��P2020��2��2����
�ʴ�Ϊ����2��2����


 Сѧ������ҵϵ�д�
Сѧ������ҵϵ�д� ��ʿһ��ȫͨϵ�д�
��ʿһ��ȫͨϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y=m��ƽ����X���ֱ�ߣ���������y=��![]() x2-4x��ֱ��y=m�ϲ�IJ�����ֱ�� y=m���ۣ����ۺ�IJ�����û�з��۵IJ�������µĺ���ͼ�����µĺ���ͼ��պ��� ֱ��y=��x��3�����㣬������������m ��ֵΪ_________
x2-4x��ֱ��y=m�ϲ�IJ�����ֱ�� y=m���ۣ����ۺ�IJ�����û�з��۵IJ�������µĺ���ͼ�����µĺ���ͼ��պ��� ֱ��y=��x��3�����㣬������������m ��ֵΪ_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����ƽ��ֱ������ϵ�У��� A ������Ϊ��6��0����AB=6![]() ���� P �ӵ� O�������߶� OA ���յ� A �˶����� P ���˶��ٶ���ÿ�� 2 ����λ���ȣ��� D ���߶� OA ���е㣮
���� P �ӵ� O�������߶� OA ���յ� A �˶����� P ���˶��ٶ���ÿ�� 2 ����λ���ȣ��� D ���߶� OA ���е㣮
��1����� B �����ꣻ
��2����� P ���˶�ʱ��Ϊ�� t �룬��BDP �����Ϊ S���� S �� t �ĺ�����ϵʽ��
��3������ P ��� D �غ�ʱ������ BP���� E ���߶� AB �ϣ����� PE������BPE=2��OBP ʱ�� ��� E �����꣮
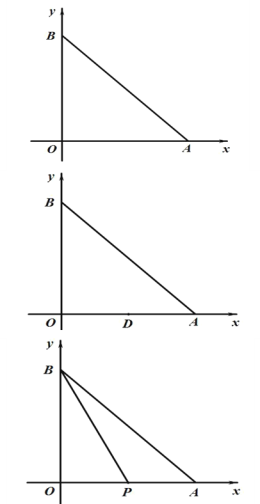
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��ij��ѧ������һ��С�����ڼ�Ķȼ�������е��飬�������ռ������ݻ�����������������ͳ��ͼ���������ͼ���ṩ����Ϣ�����������⣺

��1������ð�ѧ������������
��2����ȫƵ���ֲ�ֱ��ͼ��
��3���������ͳ��ͼ�СϦ��Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����BD����BD��CD������A��AM��BD�ڵ�M������D��DN��AB�ڵ�N����DN��4����DB���ӳ�����ȡһ��P�������ABD����MAP����PAB����AP��______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ���ABC�Ķ�����ڸ���ϣ�ֱ��aΪ�Գ��ᣬA��C���ڶԳ����ϣ�
��1����ABC��ֱ��aΪ�Գ�������AB1C��
��2������BAC=30�������BAB1=______����
��3������ABB1���������______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԫ��ǰϦ����������ij���ճ������һ��ɱ�10Ԫ/���Ĺ���ƷͶ���г�����.�������֣�ÿ��������y�����������۵���x��Ԫ/����֮��Ĺ�ϵ�ɽ��Ƶؿ���һ�κ�����y=-10x+700. ������=�����ܼ�-�ɱ��ܼۣ�
�� ����ó���Ҫÿ����5000Ԫ��������ô���۵���Ӧ��Ϊ����Ԫ/����
�� �����۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�
�� ��������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���38Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һ���������ŵ����Ų��ֵ�ʾ��ͼ������ͨ�������λ���ƽ�в���������37���ǵ�¥��AD�� BE��һ��ˮƽƽ̨DE��������֪���Ÿ߶�BC��4.8��������ˮƽ���AC=8����
��1����ˮƽƽ̨DE�ij�����
��2��������洹ֱ��ƽ̨����MN�ĸ߶�Ϊ3����������¥��AD��BE�ij���֮����
�����sin37��=0.60��cos37��=0.80��tan37��=0.75��
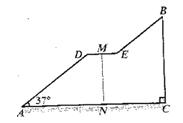
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�羰��������Ʊ���շѱ���30������(��30��)��ÿ��25Ԫ������30�ˣ���������ÿ��10Ԫ��
��1��д��Ӧ����Ʊ��![]() (Ԫ)����������
(Ԫ)����������![]() (��)֮��ĺ�����ϵʽ��
(��)֮��ĺ�����ϵʽ��
��2�����ã�1���еĺ�����ϵʽ���㣬ij��54��ȥ�÷羰������ʱ��Ϊ����Ʊ�����˶���Ԫ��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com