
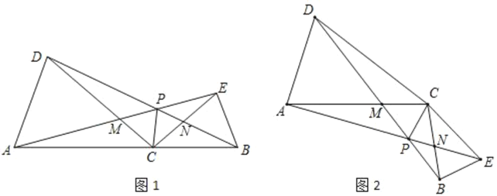
����Ŀ����ͼ1����CΪ�߶�AB������һ�㣨�����A��B�غϣ����ֱ���AC��BCΪһ����AB��ͬ����������ACD�͡�BCE��CA��CD��CB��CE����ACD����BCE��30�㣬����AE��CD�ڵ�M������BD��CE�ڵ�N��AE��BD���ڵ�P������CP��
��1���߶�AE��DB��������ϵΪ�� ����ֱ��д����APD���� ��
��2������BCE�Ƶ�C��ת����ͼ2��ʾ��λ�ã������������䣬̽���߶�AE��DB��������ϵ����˵�����ɣ������ʱ��APD�Ķ�����
��3���ڣ�2������������֤����APC����BPC��
���𰸡���1��AE��BD��30�㣻��2�����ۣ�AE��BD����APD��30�㣮���ɼ���������3��������.
��������
��1��ֻҪ֤����ACE�ա�DCB�����ɽ�����⣻
��2��ֻҪ֤����ACE�ա�DCB�����ɽ�����⣻
��3����ͼ2-1�У��ֱ��C��CH��AE������ΪH������C��CG��BD������ΪG�����������֤��CG=CH�������ý�ƽ���ߵ��ж�����֤����DPC=��EPC���ɽ�����⣻
��1���⣺��ͼ1�У�
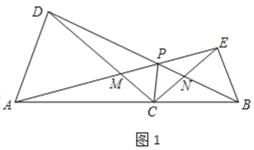
�ߡ�ACD����BCE��
���ACD+��DCE����BCE+��DCE��
���ACE����DCB��
�֡�CA��CD��CE��CB��
���ACE�ա�DCB��
��AE��BD����CAE����CDB��
�ߡ�AMC����DMP��
���APD����ACD��30����
�ʴ�ΪAE��BD��30��
��2����ͼ2�У����ۣ�AE��BD����APD��30����
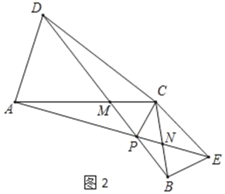
���ɣ��ߡ�ACD����BCE��
���ACD+��DCE����BCE+��DCE��
���ACE����DCB��
�֡�CA��CD��CE��CB��
���ACE�ա�DCB��
��AE��BD����CAE����CDB��
�ߡ�AMP����DMC��
���APD����ACD��30����
��3����ͼ2��1�У��ֱ��C��CH��AE������ΪH������C��CG��BD������ΪG��
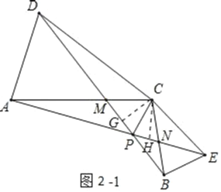
�ߡ�ACE�ա�DCB��
��AE��BD��
��S��ACE��S��DCB
��CH��CG��
���DPC����EPC
�ߡ�APD����BPE��
���APC����BPC��


 ͬ����ϰǿ����չϵ�д�
ͬ����ϰǿ����չϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AB=AC����BC��BD���ڵ�ֱ���۵���ʹ��C����AB���ϵ�E�㴦��
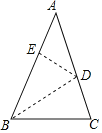
(1)����ADE=30�������BDC�Ķ�����
(2)��AB=AC=8��BC=5����������AED���ܳ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����BD����BD��CD������A��AM��BD�ڵ�M������D��DN��AB�ڵ�N����DN��4����DB���ӳ�����ȡһ��P�������ABD����MAP����PAB����AP��______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ԫ��ǰϦ����������ij���ճ������һ��ɱ�10Ԫ/���Ĺ���ƷͶ���г�����.�������֣�ÿ��������y�����������۵���x��Ԫ/����֮��Ĺ�ϵ�ɽ��Ƶؿ���һ�κ�����y=-10x+700. ������=�����ܼ�-�ɱ��ܼۣ�
�� ����ó���Ҫÿ����5000Ԫ��������ô���۵���Ӧ��Ϊ����Ԫ/����
�� �����۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ����������������Ƕ��٣�
�� ��������۲��Ź涨���ù���Ʒ���۵�����߲��ܳ���38Ԫ/������ô���۵��۶�Ϊ����ʱ�����ճ������ù���Ʒÿ���õ��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
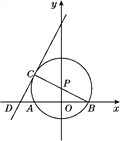
����Ŀ����ͼ����P��y��������P��x����A��B����������BP���ӳ�����P�ڵ�C������C��ֱ��y��2x��b��x���ڵ�D���ҡ�P�İ뾶Ϊ![]() ��AB��4.
��AB��4.
(1)���B��P��C�����ꣻ
(2)��֤��CD�ǡ�P��������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
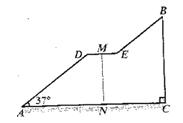
����Ŀ����ͼ��һ���������ŵ����Ų��ֵ�ʾ��ͼ������ͨ�������λ���ƽ�в���������37���ǵ�¥��AD�� BE��һ��ˮƽƽ̨DE��������֪���Ÿ߶�BC��4.8��������ˮƽ���AC=8����
��1����ˮƽƽ̨DE�ij�����
��2��������洹ֱ��ƽ̨����MN�ĸ߶�Ϊ3����������¥��AD��BE�ij���֮����
�����sin37��=0.60��cos37��=0.80��tan37��=0.75��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
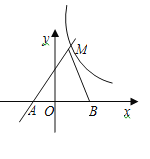
����Ŀ����ͼ��ֱ��y��kx��k��k��0����˫����![]() �ڵ�һ�������ཻ�ڵ�M����x�ύ�ڵ�A��
�ڵ�һ�������ཻ�ڵ�M����x�ύ�ڵ�A��
��1����m��ȡֵ��Χ�͵�A��������
��2������B������Ϊ��3��0����AM��5��S��ABM��8����˫���ߵĺ�������ʽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2011����Ҷ����ƺ�ݳ����Ӵ��˴������ȣ���̨�˲��ƺ�ݳ��Ľ��ij������һͣ�����Կ�����˾����������صĵ��飬���ε������������������ż���ȵ�ƺ������ѽ�ƻ�������Ⱦƣ����Ⱦƺ�������רҵ˾�����ݣ���ƽʱ�Ⱦƣ����������첻�Ⱦƣ�����ε����Ŀ������������������в�������ͳ��ͼ������������Ϣ�������������
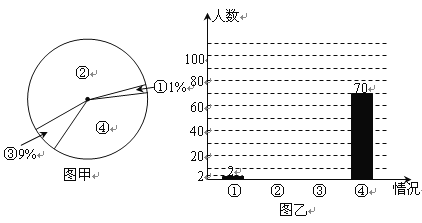
��1���ü��߱���һ�������� ��˾����
��2����ͼ�������������ε�Բ�Ľǣ�����ȫͼ�ң�
��3���ڱ��ε����У���������ɷ����е�һ��˾��������������������ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
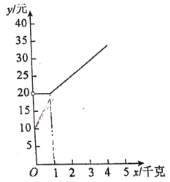
����Ŀ����һ��һ·��ս��Ϊ��Ӫ�����ҵת��Ϊ�羳�������ṩ�˻�����Ҳ�ù�������㲻�������������������Ʒ��С˿������һЩ��Ʒ�����˽���ҿ�ݹ�˾���շѷ�ʽ��
��˾����Ʒ����������1ǧ�˵ģ��踶��20Ԫ������1ǧ�˵IJ��ְ�ÿǧ��4Ԫ�Ƽۣ�
�ҹ�˾������Ʒ����ÿǧ��7Ԫ�Ƽۣ����һ�ݰ�װ��10Ԫ��
����Ʒ������Ϊ![]() ǧ�ˣ��ס��ҹ�˾��ݸ���Ʒ�ķ��÷ֱ�Ϊ
ǧ�ˣ��ס��ҹ�˾��ݸ���Ʒ�ķ��÷ֱ�Ϊ![]() ��
��
��1���![]() ��
��![]() �ĺ�������ʽ����д���Ա���
�ĺ�������ʽ����д���Ա���![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��2��ͼ�и�����![]() ��
��![]() �ĺ���ͼ������ͼ�л�����1���еĺ���ͼ��
�ĺ���ͼ������ͼ�л�����1���еĺ���ͼ��
��3��С˿��Ҫ��ݵ���Ʒ����Ϊ4ǧ�ˣ�������ʡ��ݷ��ã����ͼ��ָ����Ӧѡ��Ŀ�ݹ�˾��________��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com