
【题目】“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.
设物品的重量为![]() 千克,甲、乙公司快递该物品的费用分别为
千克,甲、乙公司快递该物品的费用分别为![]() .
.
(1)写出![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
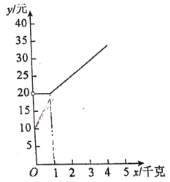
(2)图中给出了![]() 与
与![]() 的函数图象,请在图中画出(1)中的函数图象;
的函数图象,请在图中画出(1)中的函数图象;
(3)小丝需要快递的物品重量为4千克,如果想节省快递费用,结合图象指出,应选择的快递公司是________.
【答案】(1)![]() =7x+10 (x>0);(2)见解析;(3)甲.
=7x+10 (x>0);(2)见解析;(3)甲.
【解析】
(1)根据乙公司的快递费用=7×物品重量+10,即可得出![]() 与x的函数表达式;
与x的函数表达式;
(2)根据一次函数图象上点的坐标特征找出![]() 与x的函数图象经过的两点,描点、连点成线,即可画出(1)中的函数图象;
与x的函数图象经过的两点,描点、连点成线,即可画出(1)中的函数图象;
(3)根据数量关系找出![]() 与x的函数表达式,令
与x的函数表达式,令![]() =
=![]() 求出费用相等时x的值,结合函数图象即可找出结论.
求出费用相等时x的值,结合函数图象即可找出结论.
解:(1)根据题意可知:![]() 与x的函数表达式为:
与x的函数表达式为:![]() =7x+10 (x>0) .
=7x+10 (x>0) .
(2)当x=0时, ![]() =7x+10=10;当x=1时,
=7x+10=10;当x=1时,![]() =7x+10=17.
=7x+10=17.
描点、连点成线,画出函数图象,
如图所示:
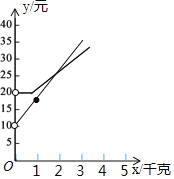
(3)根据题意可知:![]() 与x的函数表达式为:
与x的函数表达式为:
![]() .
.
当![]() =
=![]() 时,有7x+10=4x+16,
时,有7x+10=4x+16,
解得:x=2.
观察函数图象可知:当x>2时,![]() 与x的函数图象在
与x的函数图象在![]() 与x的函数图象的下方,
与x的函数图象的下方,
∴当x=4时,选择甲公司费用较低.
故答案为:甲.


科目:初中数学 来源: 题型:
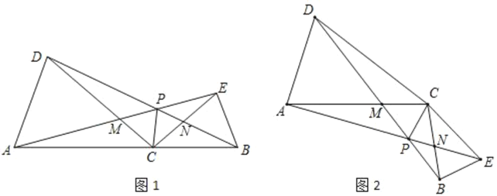
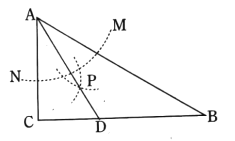
【题目】如图1,点C为线段AB上任意一点(不与点A、B重合),分别以AC、BC为一腰在AB的同侧作等腰△ACD和△BCE,CA=CD,CB=CE,∠ACD=∠BCE=30°,连接AE交CD于点M,连接BD交CE于点N,AE与BD交于点P,连接CP.
(1)线段AE与DB的数量关系为 ;请直接写出∠APD= ;
(2)将△BCE绕点C旋转到如图2所示的位置,其他条件不变,探究线段AE与DB的数量关系,并说明理由;求出此时∠APD的度数;
(3)在(2)的条件下求证:∠APC=∠BPC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在平面直角坐标系中,作出下列各点,A(-3,4), B(-3,-2),O(0,0),并把各点连起来.
(2)画出△ABO先向下平移2个单位,再向右平移4 个单位得到的图形△A1B1o1,并直接写出A1坐标
(3) 直接写出三角形ABO的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架,书中的算法体系至今仍在推动着计算机的发展和应用.《九章算术》中记载:今有户不知高、广,竿不知长、短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?译文是:今有门不知其高、宽,有竿,不知其长、短,横放,竿比门宽长出![]() 尺;竖放,竿比门高长出
尺;竖放,竿比门高长出![]() 尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为
尺;斜放,竿与门对角线恰好相等.问门高、宽、对角线长分别是多少?若设门对角线长为![]() 尺,则可列方程为__________.
尺,则可列方程为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
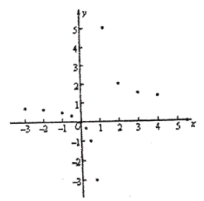
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,以
,以![]() 为圆心,任意长为半径画弧分别交
为圆心,任意长为半径画弧分别交![]() 、
、![]() 于点
于点![]() 和
和![]() ,再分别以
,再分别以![]() 、
、![]() 为圆心,大于
为圆心,大于![]() 的长为半径画弧,两弧交于点
的长为半径画弧,两弧交于点![]() ,连结
,连结![]() 并延长交
并延长交![]() 于点
于点![]() ,则下列说法中正确的个数是( )
,则下列说法中正确的个数是( )
①![]() 是
是![]() 的平分线;②
的平分线;②![]() ;③点
;③点![]() 在
在![]() 的垂直平分线上;④
的垂直平分线上;④![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象经过A(-1,0)、B(4,5)三点.
的图象经过A(-1,0)、B(4,5)三点.
(1)求此二次函数的解析式;
(2)当x为何值时,y随x的增大而减小?
(3)当x为何值时,y>0?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于关于x的二次函数y=x2-2mx-3,有下列说法:① 它的图象与x轴有两个公共点; ② 如果当x≤1时y随x的增大而减小,则m=1; ③ 如果将它的图象向左平移3个单位后过原点,则m=-1; ④ 如果当x=5时的函数值与x=2012时的函数值相等,则当x=2017时的函数值为-3.其中正确的说法有______.(填序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①△CF=2AF;②tan∠CAD=![]() ;③DF=DC;④AEF∽△CAB;⑤
;③DF=DC;④AEF∽△CAB;⑤![]() ,其中正确的结论有( )
,其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com