
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
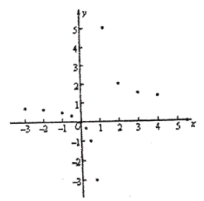
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .
 高中必刷题系列答案
高中必刷题系列答案科目:初中数学 来源: 题型:
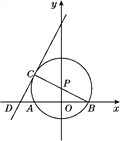
【题目】如图,点P在y轴上,⊙P交x轴于A,B两点,连接BP并延长交⊙P于点C,过点C的直线y=2x+b交x轴于点D,且⊙P的半径为![]() ,AB=4.
,AB=4.
(1)求点B,P,C的坐标;
(2)求证:CD是⊙P的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,∠A=∠FDE=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
(1) 如图 (1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
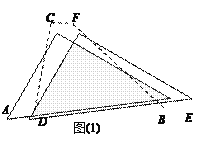
(2)如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

(3)如图(3),△DEF的F点固定在AB的中点,然后绕F点按顺时针方向旋转△DEF,使EF交在AC边上于M,FD交BC于N,若FM=x,FN=y,试求y关于x的函数关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
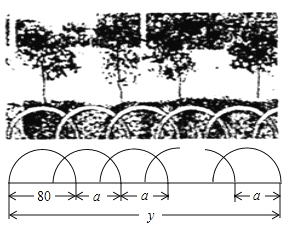
【题目】如图所示,某花园护栏是用直径为![]() 的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度增加
的半圆形条钢组制而成,且每增加一个半圆形条钢,护栏长度增加![]() ,设半圆形条钢的个数为
,设半圆形条钢的个数为![]() (
(![]() 为正整数),护栏总长度为
为正整数),护栏总长度为![]() .
.
(1)若![]() .
.
①当![]() 时,y=______
时,y=______![]() ;
;
②写出![]() 与
与![]() 之间的函数关系式为_______.
之间的函数关系式为_______.
(2)若护栏总长度为![]() ,则当
,则当![]() 时,所用半圆形条钢个数为_______;
时,所用半圆形条钢个数为_______;
(3)若护栏总长度不变,则当![]() 时,用了
时,用了![]() 个半圆形条钢;当
个半圆形条钢;当![]() 时,用了
时,用了![]() 个半圆形条钢.请求出
个半圆形条钢.请求出![]() 与
与![]() 之间的关系式.
之间的关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们约定,在平面直角坐标系![]() 中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点
中,经过象限内某点且平行于坐标轴或平行于两坐标轴夹角平分线的直线,叫该点的“参照线”.例如,点![]() 的参照线有:
的参照线有:![]() ,
,![]() ,
,![]() ,
,![]() (如图1).
(如图1).
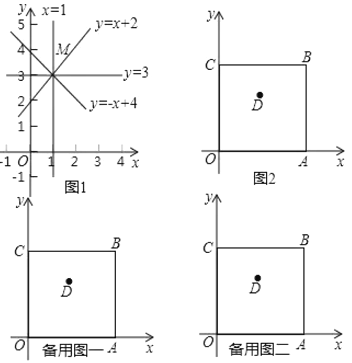
如图2,正方形![]() 在平面直角坐标系
在平面直角坐标系![]() 中,点
中,点![]() 在第一象限,点
在第一象限,点![]() ,
,![]() 分别在
分别在![]() 轴和
轴和![]() 轴上,点
轴上,点![]() 在正方形内部.
在正方形内部.
(1)直接写出点![]() 的所有参照线: ;
的所有参照线: ;
(2)若![]() ,点
,点![]() 在线段
在线段![]() 的垂直平分线上,且点
的垂直平分线上,且点![]() 有一条参照线是
有一条参照线是![]() ,则点
,则点![]() 的坐标是_______________;
的坐标是_______________;
(3)在(2)的条件下,点![]() 是
是![]() 边上任意一点(点
边上任意一点(点![]() 不与点
不与点![]() ,
,![]() 重合),连接
重合),连接![]() ,将
,将![]() 沿着
沿着![]() 折叠,点
折叠,点![]() 的对应点记为
的对应点记为![]() .当点
.当点![]() 在点
在点![]() 的平行于坐标轴的参照线上时,写出相应的折痕
的平行于坐标轴的参照线上时,写出相应的折痕![]() 所在直线的解析式: .
所在直线的解析式: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.
设物品的重量为![]() 千克,甲、乙公司快递该物品的费用分别为
千克,甲、乙公司快递该物品的费用分别为![]() .
.
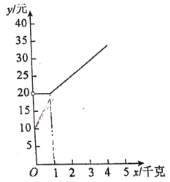
(1)写出![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(2)图中给出了![]() 与
与![]() 的函数图象,请在图中画出(1)中的函数图象;
的函数图象,请在图中画出(1)中的函数图象;
(3)小丝需要快递的物品重量为4千克,如果想节省快递费用,结合图象指出,应选择的快递公司是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得﹣1分.
(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?
(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CD=CE,△ACB的顶点A在△ECD的斜边DE上,连接BD.

(1)求证:BD=AE;
(2)若AE=5cm,AD=7cm,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com