
【题目】如图,在等边![]() 中,
中,![]() 分别为
分别为![]() 的中点,延长
的中点,延长![]() 至点
至点![]() ,使
,使![]() ,连结
,连结![]() 和
和![]() .
.
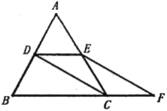
(1)求证:![]()
(2)猜想:![]() 的面积与四边形
的面积与四边形![]() 的面积的关系,并说明理由.
的面积的关系,并说明理由.
【答案】(1)见解析;(2)相等,理由见解析.
【解析】
(1)直接利用三角形中位线定理得出DE∥BC,且DE=![]() BC,再利用平行四边形的判定方法得出答案;
BC,再利用平行四边形的判定方法得出答案;
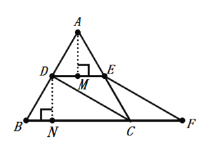
(2)分别过点A,D,作AM⊥DE,DN⊥BC,根据等底等高的三角形面积相等求得S△ADE=S△ECF,再根据S△ADE +S四边形BDEC=S△ECF +S四边形BDEC可得出结果.
(1)证明:∵D,E分别为AB,AC的中点,
∴DE是△ABC的中位线,
∴DE∥BC,DE=![]() BC.
BC.
∵CF=![]() BC,
BC,
∴DE∥CF,DE=CF,
∴四边形DEFC为平行四边形,
∴CD=EF;
(2)解:相等.理由如下:
分别过点A,D,作AM⊥DE,DN⊥BC,则∠AMD=∠DNB=90°,
∵DE∥BC,
∴∠ADM=∠DBN.
∵AD=DB,
∴△ADM≌△DBN(AAS),
∴AM=DN.
又∵DE=CF,
∴S△ADE=S△ECF (等底等高的三角形面积相等).
∴S△ADE +S四边形BDEC=S△ECF +S四边形BDEC,
∴△ABC的面积等于四边形BDEF的面积.


科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整:
的图象和性质进行了探究,探究过程如下,请补充完整:
(1)自变量![]() 的取值范围是__________;
的取值范围是__________;
(2)下表是![]() 与
与![]() 的几组对应数值:
的几组对应数值:
| … |
|
|
|
| 0 |
|
|
|
| 2 | 3 | 4 | … |
| … |
|
|
|
| 0 |
|
|
|
| 2 |
|
| … |
①写出![]() 的值为 ;
的值为 ;
②在平面直角坐标系中,描出了以表中各对对应值为坐标的点,根据描出的点,画出该函数的图象:
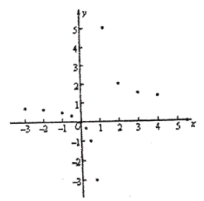
(3)当![]() 时,直接写出x的取值范围为: .
时,直接写出x的取值范围为: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元/件的日用品。若按每件5元的价格出售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件;假定每月的销售件数y(万件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
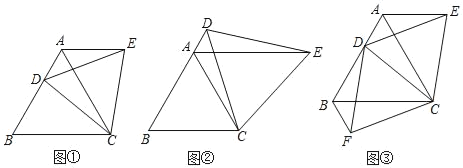
【题目】(1)操作发现:如图①,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接AE,则AE与BD有怎样的数量关系?说明理由.
(2)类比猜想:如图②,若点D是等边△ABC的边BA延长线上一动点,连接CD,以CD为边在CD上方作等边△CDE,连接AE,请直接写出AE与BD满足的数量关系,不必说明理由;
(3)深入探究:如图③,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边分别在CD上方、下方作等边△CDE和等边△CDF,连接AE,BF则AE,BF与AB有怎样的数量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①△CF=2AF;②tan∠CAD=![]() ;③DF=DC;④AEF∽△CAB;⑤
;③DF=DC;④AEF∽△CAB;⑤![]() ,其中正确的结论有( )
,其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 年巴西里约奥运会期间,南京某奥运特许经营商店以每件
年巴西里约奥运会期间,南京某奥运特许经营商店以每件![]() 元的价格购进了一批奥运纪念
元的价格购进了一批奥运纪念![]() 恤,定价为
恤,定价为![]() 元时,平均每天可售出
元时,平均每天可售出![]() 件,为了扩大销售,增加盈利,此奥运特许经营商店决定采取适当的降价措施,经调查发现,在一定范围内,奥运纪念
件,为了扩大销售,增加盈利,此奥运特许经营商店决定采取适当的降价措施,经调查发现,在一定范围内,奥运纪念![]() 恤的单价每降
恤的单价每降![]() 元,每天可多售出
元,每天可多售出![]() 件.当这种奥运纪念
件.当这种奥运纪念![]() 恤每件的价格定为多少元时,商店每天获利
恤每件的价格定为多少元时,商店每天获利![]() 元?
元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一个直角三角形纸片![]() ,
,![]() ,两直角边
,两直角边![]() ,
,![]() .
.
(1)如图1,若将![]() 沿着直线
沿着直线![]() 折叠,使顶点
折叠,使顶点![]() 与点
与点![]() 重合,求
重合,求![]() 的长;
的长;
(2)如图2,若将![]() 沿直线
沿直线![]() 折叠,使
折叠,使![]() 落在斜边
落在斜边![]() 上,且与
上,且与![]() 重合,求
重合,求![]() 的面积.
的面积.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com