
【题目】如图,在矩形ABCD中,E是AD边的中点,BE⊥AC,垂足为点F,连接DF,下面四个结论:①△CF=2AF;②tan∠CAD=![]() ;③DF=DC;④AEF∽△CAB;⑤
;③DF=DC;④AEF∽△CAB;⑤![]() ,其中正确的结论有( )
,其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
科目:初中数学 来源: 题型:
【题目】“一带一路”战略为民营快递企业转变为跨境物流商提供了机遇.也让国民可以足不出户地买到世界各国的商品.小丝购买了一些物品,并了解到两家快递公司的收费方式.
甲公司:物品重量不超过1千克的,需付费20元,超过1千克的部分按每千克4元计价.
乙公司:按物品重量每千克7元计价,外加一份包装费10元.
设物品的重量为![]() 千克,甲、乙公司快递该物品的费用分别为
千克,甲、乙公司快递该物品的费用分别为![]() .
.
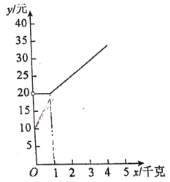
(1)写出![]() 与
与![]() 的函数表达式,并写出自变量
的函数表达式,并写出自变量![]() 的取值范围;
的取值范围;
(2)图中给出了![]() 与
与![]() 的函数图象,请在图中画出(1)中的函数图象;
的函数图象,请在图中画出(1)中的函数图象;
(3)小丝需要快递的物品重量为4千克,如果想节省快递费用,结合图象指出,应选择的快递公司是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,D是AB的中点,E在边AC上,若D与C关于BE成轴对称,则下列结论:①∠A=30°;②△ABE是等腰三角形;③点B到∠CED的两边距离相等.其中正确的有( )
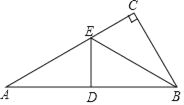
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=13 cm,AC=20 cm,BC边上的高为12 cm,则△ABC的面积是
A.126 cm2 或66 cm2B.66 cm2C.120 cm2D.126cm2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的布袋里装有4个球,其中2个红球,2个白球,它们除颜色外其余都相同.
(1)摸出1个球是白球的概率是 ;
(2)同时摸两个球恰好是两个红球的概率(要求画树状图或列表).
查看答案和解析>>
科目:初中数学 来源: 题型:
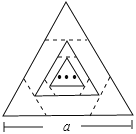
【题目】边长为a的等边三角形,记为第1个等边三角形,取其各边的三等分点,顺次连接得到一个正六边形,记为第1个正六边形,取这个正六边形不相邻的三边中点,顺次连接又得到一个等边三角形,记为第2个等边三角形,取其各边的三等分点,顺次连接又得到一个正六边形,记为第2个正六边形(如图),…,按此方式依次操作,则第6个正六边形的边长为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
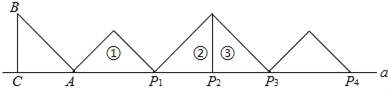
【题目】如图,等腰Rt△ABC中,∠ACB=90°,AC=BC=1,且AC边在直线a上,将△ABC绕点A顺时针旋转到位置①可得到点P1,此时AP1=![]() ;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+
;将位置①的三角形绕点P1顺时针旋转到位置②,可得到点P2,此时AP2=1+![]() ;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+
;将位置②的三角形绕点P2顺时针旋转到位置③,可得到点P3时,AP3=2+![]() …按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
…按此规律继续旋转,直至得到点P2018为止,则AP2018为( )
A. 1345+376![]() B. 2017+
B. 2017+![]() C. 2018+
C. 2018+![]() D. 1345+673
D. 1345+673![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形![]() 中,对角线
中,对角线![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 是
是![]() 上任意一点,连接
上任意一点,连接![]() ,过点
,过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,若点![]() 在
在![]() 的延长线上,
的延长线上,![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,其他条件不变,判断线段
,其他条件不变,判断线段![]() 与
与![]() 的数量关系: .
的数量关系: .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com