
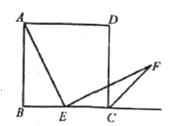
【题目】如图,四边形![]() 是正方形,点
是正方形,点![]() 是边
是边![]() 的中点,
的中点,![]() ,且
,且![]() 交正方形外角的平分线
交正方形外角的平分线![]() 于点
于点![]() ,试说明
,试说明![]() 与
与![]() 的关系.
的关系.
【答案】AE=EF,理由见解析
【解析】
取AB的中点G,连接EG,根据同角的余角相等得到∠BAE=∠CEF,证明△GAE≌△CEF即可;
AE=EF,
理由是:如图1,取AB的中点G,连接EG,则AG=BG,

∵四边形ABCD是正方形,BE=EC,
∴AG=BG=BE=EC,∠B=∠BCD=90°,
∴∠BAE+∠AEB=90°,∠BGE=45°,
∴∠AGE=135°,
∵CF是外角平分线,
∴∠DCF=45°,
∴∠ECF=135°,
∴∠AGE=∠ECF,
∵∠AEF=90°,
∴∠CEF+∠AEB=90°,
∴∠CEF=∠BAE,
在△AGE和△ECF中,
∵ ,
,
∴△AGE≌△ECF(ASA),
∴AE=EF


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:
【题目】两个全等的直角三角形ABC和DEF重叠在一起,其中∠ACB=∠DFE=90°,∠A=∠FDE=60°,AC=1. 固定△ABC不动,将△DEF进行如下操作:
(1) 如图 (1),△DEF沿线段AB向右平移(即D点在线段AB内移动),连结DC、CF、FB,四边形CDBF的形状在不断的变化,但它的面积不变化,请求出其面积.
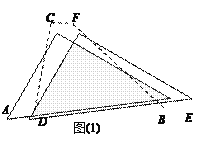
(2)如图(2),当D点移到AB的中点时,请你猜想四边形CDBF的形状,并说明理由.

(3)如图(3),△DEF的F点固定在AB的中点,然后绕F点按顺时针方向旋转△DEF,使EF交在AC边上于M,FD交BC于N,若FM=x,FN=y,试求y关于x的函数关系式。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校积极推进“阳光体育”工程,本学期在九年级11个班中开展篮球单循环比赛(每个班与其它班分别进行一场比赛,每班需进行10场比赛).比赛规则规定:每场比赛都要分出胜负,胜一场得3分,负一场得﹣1分.
(1)如果某班在所有的比赛中只得14分,那么该班胜负场数分别是多少?
(2)假设比赛结束后,甲班得分是乙班的3倍,甲班获胜的场数不超过5场,且甲班获胜的场数多于乙班,请你求出甲班、乙班各胜了几场.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ACB和△ECD都是等腰直角三角形,CA=CB,CD=CE,△ACB的顶点A在△ECD的斜边DE上,连接BD.

(1)求证:BD=AE;
(2)若AE=5cm,AD=7cm,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,D是AB的中点,E在边AC上,若D与C关于BE成轴对称,则下列结论:①∠A=30°;②△ABE是等腰三角形;③点B到∠CED的两边距离相等.其中正确的有( )
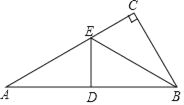
A. 0个B. 1个C. 2个D. 3个
查看答案和解析>>
科目:初中数学 来源: 题型:
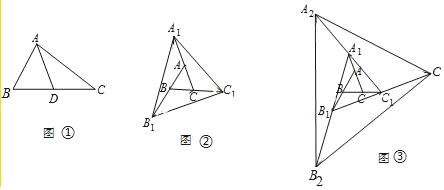
【题目】如图①,△ABC中,AD为BC边上的中线,则有S△ABD=S△ACD,许多面积问题可以转化为这个基本模型解答.如图②,已知△ABC的面积为1,把△ABC各边均顺次延长一倍,连结所得端点,得到△A1B1C1,即将△ABC向外扩展了一次,则扩展一次后的△A1B1C1的面积是_____,如图③,将△ABC向外扩展了两次得到△A2B2C2,……,若将△ABC向外扩展了n次得到△AnBnn,则扩展n次后得到的△AnBnn面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加利润,尽量减少库存,商场决定采取适当的降价措施.经调查发现,如果每件衬衫每降价2元,商场平均每天可多售出5件.求:
(1)若商场平均每天要赢利1400元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com