
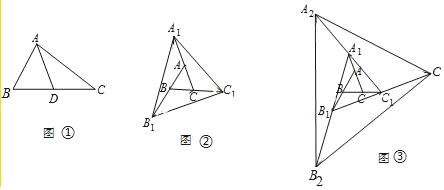
【题目】如图①,△ABC中,AD为BC边上的中线,则有S△ABD=S△ACD,许多面积问题可以转化为这个基本模型解答.如图②,已知△ABC的面积为1,把△ABC各边均顺次延长一倍,连结所得端点,得到△A1B1C1,即将△ABC向外扩展了一次,则扩展一次后的△A1B1C1的面积是_____,如图③,将△ABC向外扩展了两次得到△A2B2C2,……,若将△ABC向外扩展了n次得到△AnBnn,则扩展n次后得到的△AnBnn面积是_____.
 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有只有颜色不同的黑、白两种球共40个,小颖做摸球实验,她将盒子里面的球搅匀后从中随机摸出一个球记下颜色,再把它放回盒子中,不断重复上述过程,下表是“摸到白球”的频率折线统计图:

(1)请估计:当![]() 很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率
很大时,摸到白球的频率将会接近 (精确到0.01);假如你摸一次,你摸到白球的概率![]() .
.
(2)试估算盒子里白、黑两种颜色的球各有多少只?
(3)在(2)条件下如果要使摸到白球的概率为![]() ,需要往盒子里再放入多少个白球?
,需要往盒子里再放入多少个白球?
查看答案和解析>>
科目:初中数学 来源: 题型:
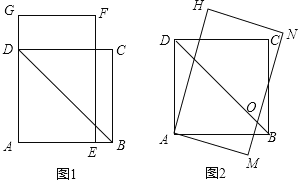
【题目】如图1,四边形ABCD是边长为![]() 的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
的正方形,矩形AEFG中AE=4,∠AFE=30°。将矩形AEFG绕点A顺时针旋转15°得到矩形AMNH(如图2),此时BD与MN相交于点O.
(1)求∠DOM的度数;
(2)图2中,求D、N两点间的距离;
(3)若将矩形AMNH绕点A再顺时针旋转15°得到矩形APQR,此时点B在矩形APQR的内部、外部还是边上?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一批单价为4元/件的日用品。若按每件5元的价格出售,每月能卖出3万件;若按每件6元的价格销售,每月能卖出2万件;假定每月的销售件数y(万件)与价格x(元/件)之间满足一次函数关系.
(1)试求y与x的函数关系式;
(2)当销售价格定为多少时,才能使每月的利润最大?每月的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
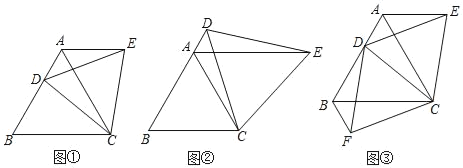
【题目】(1)操作发现:如图①,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边在CD上方作等边△CDE,连接AE,则AE与BD有怎样的数量关系?说明理由.
(2)类比猜想:如图②,若点D是等边△ABC的边BA延长线上一动点,连接CD,以CD为边在CD上方作等边△CDE,连接AE,请直接写出AE与BD满足的数量关系,不必说明理由;
(3)深入探究:如图③,点D是等边△ABC的边AB上一动点(点D与点B不重合),连接CD,以CD为边分别在CD上方、下方作等边△CDE和等边△CDF,连接AE,BF则AE,BF与AB有怎样的数量关系?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人玩赢卡片游戏,工具是一个如图所示的转盘(等分成8份),游戏规定:自由转动的转盘,当转盘停止后指针指向字母“A”,则甲输给乙2张卡片,若指针指向字母“B”,则乙输给甲3张卡片;若指针指向字母“C”,则乙输给甲1张卡片(如果指针恰好指在分割线上,那么重转一次,直到指针指向某一区域为止).
(1)转动一次转盘,求甲赢取1张卡片的概率;
(2)转动一次转盘,求乙赢取2张卡片的概率;
(3)转动一次转盘,求甲赢取卡片的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com