
【题目】如图,已知锐角△ABC内接于⊙O,连接AO并延长交BC于点D.
(1)求证:∠ACB+∠BAD=90°;
(2)过点D作DE⊥AB于E,若∠ADC=2∠ACB.求证:AC=2DE.

【答案】(1)证明见解析;(2)证明见解析
【解析】试题分析:(1)延长AD交⊙O于点F,连接BF.根据直径对的圆周角是直角得出∠ABF=90°,∠AFB +∠BAD=90°,同弧所对的圆周角相等∠AFB=∠ACB,即可证明.
(2)如图2中,过点O作OH⊥AC于H,连接BO.证明![]() 即可解决问题.
即可解决问题.
试题解析:(1)证明:延长AD交⊙O于点F,连接BF.
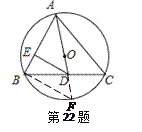
∵AF为⊙O的直径,
∴∠ABF=90°,
∴∠AFB +∠BAD=90°,
∵∠AFB=∠ACB,
∴∠ACB+∠BAD=90°.
(2)证明:如图2中,过点O作OH⊥AC于H,连接BO.
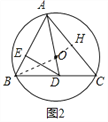
∵∠AOB=2∠ACB,
∠ADC=2∠ACB,
∴∠AOB=∠ADC,
∴∠BOD=∠BDO,
∴BD=BO,
∴BD=OA,
∵∠BED=∠AHO,∠ABD=∠AOH,
∴△BDE≌△AOH,
∴DE=AH,
∵OH⊥AC,
∴AH=CH=AC,∴AC=2DE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(-1,0),B(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.(提示:平行四边形的面积=底×高)
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化,若不变请求出该值,若会变请并请说明理由.
的值是否发生变化,若不变请求出该值,若会变请并请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)已知(a+b)2=7,(a-b)2=4,求a2+b2和ab的值.
(2)分解因式:
①x2-8xy+16y2
②(x+y+1)2-(x-y+1)2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红用一张长方形纸片ABCD进行折纸,已知该纸片宽AB为8cm,长BC为10cm.当小红折叠时,顶点D落在BC边上的点F处(折痕为AE).想一想,此时EC有多长?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,△ABC中,AD为BC边上的中线,则有S△ABD=S△ACD,许多面积问题可以转化为这个基本模型解答.如图②,已知△ABC的面积为1,把△ABC各边均顺次延长一倍,连结所得端点,得到△A1B1C1,即将△ABC向外扩展了一次,则扩展一次后的△A1B1C1的面积是_____,如图③,将△ABC向外扩展了两次得到△A2B2C2,……,若将△ABC向外扩展了n次得到△AnBnn,则扩展n次后得到的△AnBnn面积是_____.
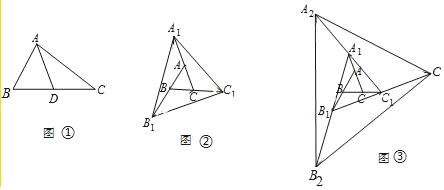
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为D.
的顶点为D.
(1)求点D的坐标(用含m的代数式表示);
(2)若该抛物线经过点A(1,m),求m的值;
(3)在(2)的条件下,抛物线与x轴是否有交点,若有,求出交点坐标,若没有,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A ,D,B,E在同一条直线上,且AD = BE, AC = DF,补充下列其中一个条件后,不一定能得到△ABC≌△DEF 的是( )

A.BC = EFB.AC//DFC.∠C = ∠FD.∠BAC = ∠EDF
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.

(1)如果AC=6cm,BC=8cm,试求△ACD的周长;
(2)如果∠CAD:∠BAD=1:2,求∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com