
【题目】如图,四边形 ABCD 是正方形,点 E,H 分别在 BC,AB 上,点 G 在 BA 的延长线上, 且 CE=AG,DE⊥CH 于 F.
(1)求证:四边形 GHCD 为平行四边形.
(2)在不添加任何辅助线的情况下,请直接写出图中所有与∠ECF 互余的角.
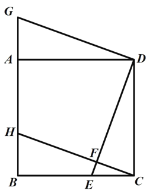
【答案】(1)见解析;(2)∠FEC,∠BHC,∠BGD,∠ADE,∠HCD
【解析】
(1)先证△ECD≌△GAD,得到∠EDC=∠ADG,再推到GD∥HC,从而证平行四边形;
(2)利用矩形顶角为90°,HC⊥ED,可推导∠BHC,∠HCD,∠FEC与∠ECF互余,再利用△ECD≌△GAD,可以推导得到∠BGD,∠ADE与∠ECF互余.
∵四边形ABCD是正方形,∴∠ECD=∠GAD=90°,CD=AD,HG∥CD
∵EC=AG
在△ECD和△GAD
∴△ECD≌△GAD(SAS)
∴∠EDC=∠GDA
∵∠ADE+∠EDC=90°
∴∠GDA+∠ADE=90°
∵HC⊥ED,∴∠HFD=90°
∴GD∥HC
∴四边形GHCD是平行四边形
(2)∵∠BCD=90°,∴∠HCD与∠ECF互余
∵ED⊥HC,∴∠FEC与∠ECF互余
∵∠B=90°,∴∠BHC与∠ECF互余
∵△ECD≌△GAD,∴∠BGD=∠CED,∴∠BGD与∠ECF互余
∵已证∠GDF=90°,∴∠ADE与∠ECF互余


科目:初中数学 来源: 题型:
【题目】点A为双曲线y=![]() (k≠0)上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为( )
(k≠0)上一点,B为x轴上一点,且△AOB为等边三角形,△AOB的边长为2,则k的值为( )
A. 2![]() B. ±2
B. ±2![]() C.
C. ![]() D. ±
D. ±![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一商店销售某种商品,平均每天可售出20件,每件盈利40元.为了扩大销售,增加盈利,该店采取了降价措施.在每件盈利不少于25元的前提下,经过一段时间销售,发现销售单价每降低1元,平均每天可多售出2件.
(1)若降价4元,则平均每天销售数量为 件;
(2)当每件商品降价多少元时,该商店每天销售利润为1050元?
查看答案和解析>>
科目:初中数学 来源: 题型:
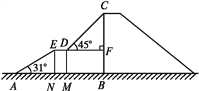
【题目】下图是某儿童乐园为小朋友设计的滑梯平面图.已知BC=4 m,AB=6 m,中间平台宽度DE=1 m,EN,DM,CB为三根垂直于AB的支柱,垂足分别为N,M,B,∠EAB=31°,DF⊥BC于点F,∠CDF=45°,求DM和BC的水平距离BM的长度.(结果精确到0.1 m.参考数据:sin 31°≈0.52,cos 31°≈0.86,tan 31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲乙两人买了相同数量的信封和信笺,甲每发一封信都只用1张信笺,乙每发一封信都要用3张信笺,结果甲用掉了所有的信封,但余下50张信笺,而乙用掉了所有的信笺,但余下50个信封.
(1)求甲乙两人各买的信封和信笺的数量分别为多少?
(2)若甲乙两人每发出一封信需邮费5元,求甲乙各用去多少元邮费?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由于“哈啰小蓝车”的投放使用,自行车正逐渐成为人们喜爱的交通工具.某商城的自行车销售量自 2019 年起逐月增加,据统计,该商城 9 月份销售自行车 64 辆,11 月份销售了 100 辆;
(1)若该商城 9 月至 11 月的自行车销售的月平均增长率相同,求自行车销售的月平均增长率.
(2)考虑到自行车需求不断增加,该商城准备再购进一批两种规格的自行车共 100 辆,已知 A 型车的进价为每辆 500 元,售价为每辆 700 元,B 型车的进价为每辆 1000 元,售价为每辆 1300 元.假设所购进车辆全部售完,为使利润不低于 26000 元,该商城购进 A 型车不超过多少辆?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】大家见过形如x+y=z,这样的三元一次方程,并且知道x=3,y=4,z=7就是适合该方程的一个正整数解,法国数学家费尔马早在17世纪还研究过形如x2+y2=z2的方程.
(1)请写出方程x2+y2=z2的两组正整数解: .
(2)研究直角三角形和勾股数时,我国古代数学专著(九章算术)给出了如下数:a=![]() (m2﹣n2),b=mn,c=
(m2﹣n2),b=mn,c=![]() (m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
(m2+n2),(其中m>n,m,n是奇数),那么,以a,b,c为三边的三角形为直角三角形,请你加以验证.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,E是正方形ABCD的边AB上的动点,EF⊥DE交BC于点F.
(1)求证:△ADE∽△BEF.
(2)设正方形的边长为4,AE=x,BF=y.当x取什么值时,y有最大值?并求出这个最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,对角线AC,BD相交于点O,AB⊥AC,AB=3cm,BC=5cm.点P从A点出发沿AD方向匀速运动,速度为1cm/s,连接PO并延长交BC于点Q.设运动时间为t(s)(0<t<5)
(1)当t为何值时,四边形ABQP是平行四边形?
(2)当t=3时四边形OQCD的面积为多少?
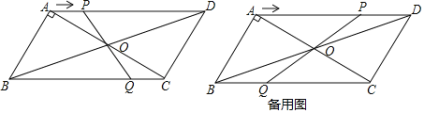
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com