
【题目】△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
(1)如图①,当点C与点O重合时,求直线BD的表达式;
(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;
(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2![]() )时,求∠ODB的正切值.
)时,求∠ODB的正切值.

 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数 ______ .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于![]() ,
,![]() 的方程组
的方程组![]() ,则下列结论中:①当
,则下列结论中:①当![]() 时,方程组的解是
时,方程组的解是![]() ;②当
;②当![]() ,
,![]() 的值互为相反数时,
的值互为相反数时,![]() ;③不存在一个实数
;③不存在一个实数![]() 使得
使得![]() ;④若
;④若![]() ,则
,则![]() 正确的个数有( )
正确的个数有( )
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc<0;②b2﹣4ac=0;③a>2;④4a﹣2b+c>0.其中正确结论的个数是( )
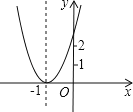
A.1 B.2 C.3 D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(图①为实景侧视图,图②为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平线夹角为θ1,且在水平线上的射影AF为1.4 m.现已测量出屋顶斜面与水平面夹角为θ2,并已知tan θ1=1.082,tan θ2=0.412.如果安装工人已确定支架AB高为25 cm,求支架CD的高.(结果精确到1 cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线![]() 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )

A. 24 B. 23 C. 22 D. 21
查看答案和解析>>
科目:初中数学 来源: 题型:
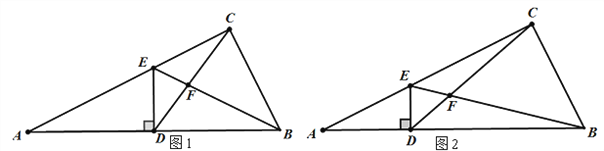
【题目】如图1,点D为直角三角形ABC的斜边AB上的中点,DE⊥AB交AC于E, 连EB、CD,线段CD与BF交于点F.若tanA=![]() ,则
,则![]() =_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若
=_____.如图2,点D为直角三角形ABC的斜边AB上的一点,DE⊥AB交AC于E, 连EB、CD;线段CD与BF交于点F.若![]() ,tanA=
,tanA=![]() ,则
,则![]() =____.
=____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 的解析式是
的解析式是![]() ,并且与
,并且与![]() 轴、
轴、![]() 轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着
轴分别交于A、B两点.一个半径为1.5的⊙C,圆心C从点(0,1.5)开始以每秒0.5个单位的速度沿着![]() 轴向下运动,当⊙C与直线
轴向下运动,当⊙C与直线![]() 相切时,则该圆运动的时间为( )
相切时,则该圆运动的时间为( )
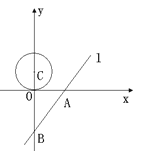
A. 3秒或6秒 B. 6秒 C. 3秒 D. 6秒或16秒
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为A(-1,0),B(3,0),现同时将点A,B分别向上平移2个单位,再向右平移1个单位,分别得到点A,B的对应点C,D,连接AC,BD,CD.
(1)求点C,D的坐标及四边形ABDC的面积S四边形ABDC.(提示:平行四边形的面积=底×高)
(2)在y轴上是否存在一点P,连接PA,PB,使S△PAB=S四边形ABDC?若存在这样一点,求出点P的坐标;若不存在,试说明理由.
(3)点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合)![]() 的值是否发生变化,若不变请求出该值,若会变请并请说明理由.
的值是否发生变化,若不变请求出该值,若会变请并请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com