练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，点P是等边三角形ABC内一点，且PA=3，PB=4，PC=5，若将△APB绕着点B逆时针旋转后得到△CQB，则∠APB的度数 ______ ．

    【答案】150°

    【解析】连接PQ，由题意可知△ABP≌△CBQ

    则QB=PB=4，PA=QC=3，∠ABP=∠CBQ，

    ∵△ABC是等边三角形，

    ∴∠ABC=∠ABP+∠PBC=60°，

    ∴∠PBQ=∠CBQ+∠PBC=60°，

    ∴△BPQ为等边三角形，

    ∴PQ=PB=BQ=4，

    又∵PQ=4，PC=5，QC=3，

    ∴PQ2+QC2=PC2，

    ∴∠PQC=90°，

    ∵△BPQ为等边三角形，

    ∴∠BQP=60°，

    ∴∠BQC=∠BQP+∠PQC=150°

    ∴∠APB=∠BQC=150°

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

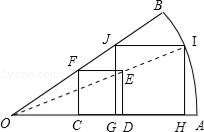
    【题目】小明手上一张扇形纸片OAB．现要求在纸片上截一个正方形，使它的面积尽可能大．

    小明的方案是：如图，在扇形纸片OAB内，画正方形CDEF，使C、D在OA上，F在OB上；连接OE并延长交弧AB于I，画IH∥ED交OA于H，IJ∥OA交OB于J，再画JG∥FC交OA于G．

    （1）你认为小明画出的四边形GHIJ是正方形吗？如果是，请证明．如果不是，请说明理由．

    （2）如果扇形OAB的圆心角∠AOB=30°，OA=6cm，小明截得的四边形GHIJ面积是多少（结果精确到0.1cm）．

    （3）（1）中小明画出的四边形GHIJ如果是正方形，我们把它叫做扇形的内接正方形（四个顶点分别在扇形的半径和弧上）．请你再画出一种不同于图（1）的扇形的内接正方形（保留画图痕迹，不要求证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

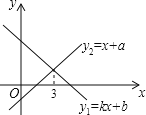
    【题目】一次函数与的图象如图，则下列结论①②，且的值随着值的增大而减小.③关于的方程的解是④当时，，其中正确的有___________．（只填写序号）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，CD为⊙O的直径，CD⊥AB，垂足为点F，AO⊥BC，垂足为点E，AO=1．

    （1）求∠C的大小；

    （2）求阴影部分的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

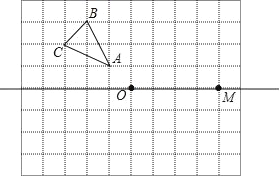
    【题目】如图，它是一个8×10的网格，每个小正方形的边长均为1，每个小正方形的顶点叫格点，△ABC的顶点均在格点上．

    （1）画出△ABC关于直线OM对称的△A1B1C1．

    （2）画出△ABC关于点O的中心对称图形△A2B2C2．

    （3）△A1B1C1与△A2B2C2组成的图形是轴对称图形吗？如果是，请画出对称轴．△A1B1C1与△A2B2C2组成的图形　 　（填“是”或“不是”）轴对称图形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一商店销售某种商品，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，该店采取了降价措施．在每件盈利不少于25元的前提下，经过一段时间销售，发现销售单价每降低1元，平均每天可多售出2件．

    （1）若降价4元，则平均每天销售数量为　 　件；

    （2）当每件商品降价多少元时，该商店每天销售利润为1050元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知△ABN和△ACM位置如图所示，AB=AC，AD=AE，∠1=∠2．

    （1）求证：BD=CE；

    （2）求证：∠M=∠N．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】甲乙两人买了相同数量的信封和信笺，甲每发一封信都只用1张信笺，乙每发一封信都要用3张信笺，结果甲用掉了所有的信封，但余下50张信笺，而乙用掉了所有的信笺，但余下50个信封．

    (1)求甲乙两人各买的信封和信笺的数量分别为多少？

    (2)若甲乙两人每发出一封信需邮费5元，求甲乙各用去多少元邮费？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).

    (1)如图①,当点C与点O重合时,求直线BD的表达式;

    (2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;

    (3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2)时,求∠ODB的正切值.

    查看答案和解析>>

    同步练习册答案