
【题目】小明手上一张扇形纸片OAB.现要求在纸片上截一个正方形,使它的面积尽可能大.
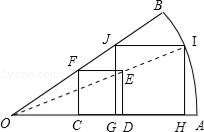
小明的方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连接OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥OA交OB于J,再画JG∥FC交OA于G.
(1)你认为小明画出的四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(2)如果扇形OAB的圆心角∠AOB=30°,OA=6cm,小明截得的四边形GHIJ面积是多少(结果精确到0.1cm).
(3)(1)中小明画出的四边形GHIJ如果是正方形,我们把它叫做扇形的内接正方形(四个顶点分别在扇形的半径和弧上).请你再画出一种不同于图(1)的扇形的内接正方形(保留画图痕迹,不要求证明)
【答案】(1)是,详见解析;(2)正方形GHIJ的面积是4.3cm2;(3)详见解析.
【解析】试题分析:(1)根据HI∥DE,JG∥FC,JI∥GH,利用矩形的判定得出四边形JGHI是矩形,进而利用平行线分线段成比例定理得出即可;
(2)正方形GHIJ的边长为x,则GH=HI=JG=x,表示出GO= ![]() ,
, ![]() ,再利用勾股定理求解;
,再利用勾股定理求解;
(3)画一个使正方形一边平行于AB的一个正方形即可.
(1)答:是.
证明:∵在扇形纸片OAB内,画正方形CDEF,IH∥ED交OA于H,
IJ∥OA交OB于J,JG∥FC交OA于G,
∴HI∥DE,JG∥FC,JI∥GH,
∴∠JGH=∠IHG=∠JIH=90°,
∴四边形JGHI是矩形,
∵HI∥DE,JG∥FC,JI∥GH,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∵FE=DE,
∴JI=HI,
∴矩形JGHI是正方形,
(2)设正方形GHIJ的边长为x,则GH=HI=JG=x,
∵∠AOB=30°,OA=6cm,
在直角三角形△OGJ,∠GOJ=30°,
∴GO=![]() x,
x,
∴HO=x+![]() x,
x,
∴![]() ,
,
x2=![]() ≈4.3,
≈4.3,
所以正方形GHIJ的面积是4.3cm2.
(3)如图:



 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】(本题满分8分)如图,在△ABC中,AB=AC,∠DAC是△ABC的一个外角.
实践与操作:
根据要求尺规作图,并在图中标明相应字母(保留作图痕迹,不写作法).

(1)作∠DAC的平分线AM;
(2)作线段AC的垂直平分线,与AM交于点F,与BC边交于点E,连接AE、CF.
猜想并证明:
判断四边形AECF的形状并加以证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是菱形,∠A=60°,AB=2,扇形BEF的半径为2,圆心角为60°,则图中阴影部分的面积是( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,连接BD,点
边上一点,连接BD,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(3)在(2)的条件下,如图3,若![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
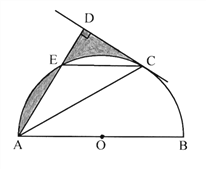
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD![]() CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离水面高度为5m的岸上有人用绳子拉船靠岸,开始绳子与水面的夹角为30°,此人以每秒0.5m的速度收绳.
(1)8秒后船向岸边移动了多少米?
(2)写出还没收的绳子的长度S米与收绳时间t秒的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P是等边三角形ABC内一点,且PA=3,PB=4,PC=5,若将△APB绕着点B逆时针旋转后得到△CQB,则∠APB的度数 ______ .

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com