
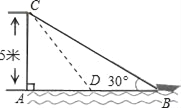
【题目】如图,在离水面高度为5m的岸上有人用绳子拉船靠岸,开始绳子与水面的夹角为30°,此人以每秒0.5m的速度收绳.
(1)8秒后船向岸边移动了多少米?
(2)写出还没收的绳子的长度S米与收绳时间t秒的函数关系式.

【答案】(1)![]() (m);(2)S=10﹣0.5t(0≤t≤10).
(m);(2)S=10﹣0.5t(0≤t≤10).
【解析】【试题分析】
(1)假设8秒后,船到达D位置,连接CD,
在Rt△ACB中,AC=5m,∠CBA=30°,根据30度所对的直角边是斜边的一半,得:CB=2AC=10m;此人以每秒0.5m的速度收绳,则8秒后收回的绳子长为:0.5×8=4m,
则CD=10﹣4=6(m);在Rt△ACD中,根据勾股定理得: AD=![]() (m);在Rt△ACB中,根据勾股定理得: AB=
(m);在Rt△ACB中,根据勾股定理得: AB=![]() (m),则BD=AB﹣AD=
(m),则BD=AB﹣AD=![]() (m);即8秒后船向岸边移动了
(m);即8秒后船向岸边移动了![]() 米.
米.
(2)原来绳子的长度为10米,以每秒0.5m的速度收绳,则t秒后剩下的绳长为(10-0.5t)米,即S=10﹣0.5t,由于绳长至少为5米,则要求0≤t≤10.
【试题解析】
(1)假设8秒后,船到达D位置,连接CD,
∵AC=5m,∠CBA=30°,
∴CB=2AC=10m,
此人以每秒0.5m的速度收绳,则8秒后收回的绳子长为:0.5×8=4m,
∴CD=10﹣4=6(m),
在Rt△ACD中: AD=![]() (m),
(m),
在Rt△ACB中:AB=![]() (m),
(m),
则BD=AB﹣AD=![]() (m);
(m);

(2)S=10﹣0.5t(0≤t≤10).


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:
【题目】新农村社区改造中,有一部分楼盘要对外销售,某楼盘共23层,销售价格如下:第八层楼房售价为4000元/米2,从第八层起每上升一层,每平方米的售价提高50元;反之,楼层每下降一层,每平方米的售价降低30元,已知该楼盘每套楼房面积均为120米2.
若购买者一次性付清所有房款,开发商有两种优惠方案:
方案一:降价8%,另外每套楼房赠送a元装修基金;
方案二:降价10%,没有其他赠送.
(1)请写出售价y(元/米2)与楼层x(1≤x≤23,x取整数)之间的函数关系式;
(2)老王要购买第十六层的一套楼房,若他一次性付清购房款,请帮他计算哪种优惠方案更加合算.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是“作已知三角形的高”的尺规作图过程.
已知: ![]() .
.

求作: ![]() 边上的高
边上的高![]()
作法:如图,
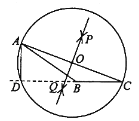
(1)分别以点![]() 和点
和点![]() 为圆心,大于
为圆心,大于![]() 的长为半径作弧,两弧相交于
的长为半径作弧,两弧相交于![]() ,
, ![]() 两点;
两点;
(2)作直线![]() ,交
,交![]() 于点
于点![]() ;
;
(3)以![]() 为圆心,
为圆心, ![]() 为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
为半径⊙O,与CB的延长线交于点D,连接AD,线段AD即为所作的高.
请回答;该尺规作图的依据是___________________________________________________
查看答案和解析>>
科目:初中数学 来源: 题型:
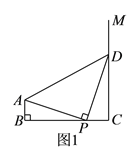
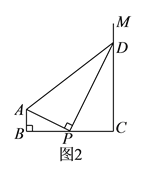
【题目】已知:如图,△ABC中,∠BAD=∠EBC,AD交BE于F.
(1)试说明 : ∠ABC=∠BFD ;
(2)若∠ABC=35°,EG∥AD,EH⊥BE,求∠HEG的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图, ![]() ,射线
,射线![]() ,且
,且![]() ,
, ![]() ,点
,点![]() 是线段
是线段![]() (不与点
(不与点![]() 、
、![]() 重合)上的动点,过点
重合)上的动点,过点![]() 作
作![]() 交射线
交射线![]() 于点
于点![]() ,连结
,连结![]() .
.
(![]() )如图
)如图![]() ,若
,若![]() ,求证:
,求证: ![]() ≌
≌![]() .
.
(![]() )如图
)如图![]() ,若
,若![]() 平分
平分![]() ,试猜测
,试猜测![]() 和
和![]() 的数量关系,并说明理由.
的数量关系,并说明理由.
(![]() )若
)若![]() 是等腰三角形,作点
是等腰三角形,作点![]() 关于
关于![]() 的对称点
的对称点![]() ,连结
,连结![]() ,则
,则![]() __________.(请直接写出答案)
__________.(请直接写出答案)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC中,AB=AC=12厘米,∠B=∠C,BC=8厘米,点D为AB的中点.如果点P在线段BC上以2厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.若点Q的运动速度为v厘米/秒,则当△BPD与△CQP全等时,v的值为________厘米/秒.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com