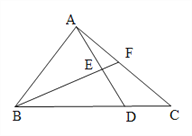
【题目】如图，△ABC的面积为49cm2，AE＝ED，BD＝3DC，则图中△AEF的面积等于___________.
【答案】
【解析】分析：过D作DG∥CA交BF于G，可以得到△AEF≌△GEG，有全等三角形的性质得到GE=EF，DG=AF．由DG∥CF，得到BG=3GF，DG：FC= 3：4，进而有AF：FC=3：4．设EF=a，则GE=a，BG=6a，BE=7a．设S△AEF=x，则S△DEG=x，S△ABE=7x，得到S△ABF=8x．由AF：FC=3：4，得到S△ABF=21，解方程即可得到结论．
详解：过D作DG∥CA交BF于G，∴∠GDE=∠DAF．∵∠GED=∠AEF，AE=ED，∴△AEF≌△GEG，∴GE=EF，DG=AF．∵BD＝3DC，DG∥CF，∴BG=3GF，△BDG∽BCF，∴DG：FC=BD：BC=3：4，∴DG=
FC，∴AF：FC=3：4．
设EF=a，则GE=a，BG=6a，BE=7a．设S△AEF=x，则S△DEG=x，S△ABE=7x，∴S△ABF=8x．∵AF：FC=3：4，∴AF：AC=3：7，∴S△ABF=
=21，∴8x=21，∴x=
．故△AEF的面积=
．故答案为： 
．
应用题作业本系列答案科目：初中数学 来源： 题型：
【题目】图
是一个可以自由转动的转盘，被分成了面积相等的三个扇形，分别标有数
， 
， 
，甲转动一次转盘，转盘停止后指针指向的扇形内的数记为
（如果指针恰好指在分割线上，那么重转一次，直到指针指向某一扇形为止）．图
是背面完全一样、牌面数字分别是
， 
， 
， 
的四张扑克牌，把四张扑克牌背面朝上，洗匀后放在桌面上，乙随机抽出一张牌的牌面数字记为
．计算
的值．
（
）用树状图或列表法求
的概率．
（
）甲乙两人玩游戏，规定：当
是正数时，甲胜；否则，乙胜，你认为这个游戏规则对甲乙双方公平吗？请说明理由．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：∠MON=80°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C不与点O 重合），连接AC交射线OE于点D．设∠OAC=x°．
（1）如图1，若AB∥ON，则：①∠ABO的度数是 ；
②如图2，当∠BAD=∠ABD时，试求x的值（要说明理由）；
（2）如图3，若AB⊥OM，则是否存在这样的X的值，使得△ADB中有两个相等的角？若存在，直接写出x的值；若不存在，说明理由．（自己画图）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某宾馆有50个房间共游客居住.当每个房间定价为180元时，房间会全部住满；当每个房间的定价增加10元时，就会有一个房间空闲．
设每个房间每天的定价增加x个10元.
（Ⅰ）填写下表：
每个房间每天定价（元） | 180 | 190 | 200 | 210 | …… | 180×10x |
住满房间个数（个） | 50 | 49 | 48 | …… |
（Ⅱ）若游客居住的房间的当天收入为y(元)，写出y关于x的函数关系式；
（Ⅲ）如果游客入住房间，宾馆需对每个房间每天支出20元的各种费用．当房间定价为多少的时候，宾馆获得的利润W（元）最大？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在离水面高度为5m的岸上有人用绳子拉船靠岸，开始绳子与水面的夹角为30°，此人以每秒0.5m的速度收绳．
（1）8秒后船向岸边移动了多少米？
（2）写出还没收的绳子的长度S米与收绳时间t秒的函数关系式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，已知抛物线C：y=x2-4x+4和直线l:y=kx-2k(k>0).
(1)抛物线C的顶点D的坐标为 ；
(2)请判断点D是否在直线
上，并说明理由；
(3)记函数
的图像为G，点M（0，t)，过点M垂直于
轴的直线与图像G交于点
.当1<t<3时，若存在t使得
成立，结合图像，求k的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com