
【题目】某次大型活动,组委会启用无人机航拍活动过程,在操控无人机时应根据现场状况调节高度,已知无人机在上升和下降过程中速度相同,设无人机的飞行高度h(米)与操控无人机的时间t(分钟)之间的关系如图中的实线所示,根据图象回答下列问题:
(1)图中的自变量是______,因变量是______;
(2)无人机在75米高的上空停留的时间是______分钟;
(3)在上升或下降过程中,无人机的速度______为米/分;
(4)图中a表示的数是______;b表示的数是______;
(5)图中点A表示______.

【答案】(1)时间(或t);高度(或h);(2)5;(3)25;(4)2;15;(5)在第6分钟时,无人机的飞行高度为50米.
【解析】
![]() 根据图象信息得出自变量和因变量即可;
根据图象信息得出自变量和因变量即可;![]() 根据图象信息得出无人机在75米高的上空停留的时间
根据图象信息得出无人机在75米高的上空停留的时间![]() 分钟即可;
分钟即可;![]() 根据速度
根据速度![]() 路程除以时间计算即可;
路程除以时间计算即可;![]() 根据速度的汽车时间即可;
根据速度的汽车时间即可;![]() 根据点的实际意义解答即可.
根据点的实际意义解答即可.
解:(1)横轴是时间,纵轴是高度,所以自变量是时间(或t),因变量是高度(或h);
(2)无人机在75米高的上空停留的时间是12-7=5分钟;
(3)在上升或下降过程中,无人机的速度![]() 米/分;
米/分;
(4)图中a表示的数是![]() 分钟;b表示的数是
分钟;b表示的数是![]() 分钟;
分钟;
(5)图中点A表示在第6分钟时,无人机的飞行高度为50米;
故答案为:时间(或t);高度(或h);5;25;2;15;在第6分钟时,无人机的飞行高度为50米.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
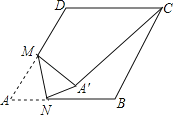
【题目】如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN沿MN所在直线翻折得到△A′MN,连接A′C,则A′C长度的最小值是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,AD是⊙O的直径,AD与BC相交于点M,且BM=MC,过点D作BC的平行线,分别与AB、AC的延长线相交于点E、F.
(1)求证:EF与⊙O相切;
(2)若BC=2![]() ,MD=
,MD=![]() ,求CE的长.
,求CE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
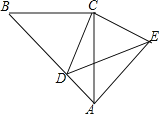
【题目】如图,△ACB与△CED都是等腰直角三角形,∠BCA=∠DCE=90°,且点D在线段AB上,连接AE.
(1)求证:①△BCD≌△ACE;②∠DAE=90°;
(2)若AB=8,当点D在线段AB上什么位置时,四边形ADCE的周长最小?请说明并求出周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人玩“石头、剪刀、布”的游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“石头”、“剪刀”、“布”的卡片张数分别为3、5、7.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“石头”胜“剪刀”,“剪刀”胜“布”,“布”胜“石头”,同种卡片不分胜负
(1)若甲先摸,则他摸出“石头”的概率是______;
(2)若甲先摸出“石头”,则乙再摸出“石头”的概率是______;
(3)若甲先摸出了“石头”,则乙获胜的概率是______;
(4)若甲先摸,则他摸出哪种卡片获胜的可能性最大?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明手上一张扇形纸片OAB.现要求在纸片上截一个正方形,使它的面积尽可能大.
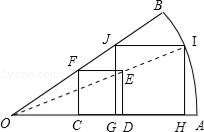
小明的方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连接OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥OA交OB于J,再画JG∥FC交OA于G.
(1)你认为小明画出的四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(2)如果扇形OAB的圆心角∠AOB=30°,OA=6cm,小明截得的四边形GHIJ面积是多少(结果精确到0.1cm).
(3)(1)中小明画出的四边形GHIJ如果是正方形,我们把它叫做扇形的内接正方形(四个顶点分别在扇形的半径和弧上).请你再画出一种不同于图(1)的扇形的内接正方形(保留画图痕迹,不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小强骑车从家到学校要经过一段先上坡后下坡的路,在这段路上小强骑车的距离s(千米)与骑车的时间t(分钟)之间的函数关系如图所示,请根据图中信息回答下列问题:

(1)小强去学校时下坡路长 千米;
(2)小强下坡的速度为 千米/分钟;
(3)若小强回家时按原路返回,且上坡的速度不变,下坡的速度也不变,那么回家骑车走这段路的时间是 分钟.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com