
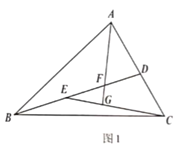
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,连接BD,点
边上一点,连接BD,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(3)在(2)的条件下,如图3,若![]() ,求线段
,求线段![]() 的长.
的长.

【答案】(1)详见解析;(2)详见解析;(3)6
【解析】
(1)根据直角三角形的性质可得![]() ,
,![]() ,然后根据三角形的内角和和已知条件即可推出结论;
,然后根据三角形的内角和和已知条件即可推出结论;
(2)根据直角三角形的性质和已知条件可得![]() ,进而可得
,进而可得![]() ,
,![]() ,然后即可根据AAS证明
,然后即可根据AAS证明![]() ≌
≌![]() ,可得
,可得![]() ,进一步即可证得结论;
,进一步即可证得结论;
(3)连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,如图4.先根据已知条件、三角形的内角和定理和三角形的外角性质推出
,如图4.先根据已知条件、三角形的内角和定理和三角形的外角性质推出![]() ,进而可得
,进而可得![]() ,然后即可根据SAS证明△ABE≌△ACH,进一步即可推出
,然后即可根据SAS证明△ABE≌△ACH,进一步即可推出![]() ,过点
,过点![]() 作
作![]() 于K,易证△AKD≌△CHD,可得
于K,易证△AKD≌△CHD,可得![]() ,然后即可根据等腰三角形的性质推得DF=2EF,问题即得解决.
,然后即可根据等腰三角形的性质推得DF=2EF,问题即得解决.
(1)证明:如图1,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ;
;
(2)证明:如图2,![]() ,
,![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
∵点![]() 为
为![]() 的中点,∴AD=CD,
的中点,∴AD=CD,![]() ,
,
![]() ≌
≌![]() (AAS),
(AAS),![]() ,
,
![]() ,
,![]() ;
;

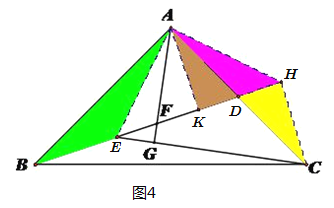
(3)解:连接![]() ,过点
,过点![]() 作
作![]() 交
交![]() 延长线于点
延长线于点![]() ,连接
,连接![]() ,如图4.
,如图4.
![]() ,
,![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,∴△ABE≌△ACH(SAS),
,∴△ABE≌△ACH(SAS),
![]() ,
,![]() ,
,
过点![]() 作
作![]() 于K,
于K,![]() ,
,
![]() ,
,![]() ,
,
∴△AKD≌△CHD(AAS),![]() ,
,
∵![]() ,
,
![]() ,
,
![]() ,
,![]() .
.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案科目:初中数学 来源: 题型:
【题目】某校计划购买篮球、排球共20个,购买2个篮球,3个排球,共需花费190元;购买3个篮球的费用与购买5个排球的费用相同。
(1)篮球和排球的单价各是多少元?
(2)若购买篮球不少于8个,所需费用总额不超过800元.请你求出满足要求的所有购买方案,并直接写出其中最省钱的购买方案
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】受气候的影响,某超市蔬菜供应紧张,需每天从外地调运蔬菜1000斤.超市决定从甲、乙两大型蔬菜棚调运蔬菜,已知甲蔬菜棚每天最多可调出800斤,乙蔬菜棚每天最多可调运600斤,从两蔬菜棚调运蔬菜到超市的路程和运费如下表:
到超市的路程(千米) | 运费(元/斤·千米) | |
甲蔬菜棚 | 120 | 0.03 |
乙蔬菜棚 | 80 | 0.05 |
(1)若某天调运蔬菜的总运费为3840元,则从甲、乙两蔬菜棚各调运了多少斤蔬菜?
(2)设从甲蔬菜棚调运蔬菜![]() 斤,总运费为
斤,总运费为![]() 元,试写出
元,试写出![]() 与
与![]() 的函数关系式,怎样安排调运方案才能使每天的总运费最省?
的函数关系式,怎样安排调运方案才能使每天的总运费最省?
查看答案和解析>>
科目:初中数学 来源: 题型:
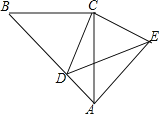
【题目】如图,△ACB与△CED都是等腰直角三角形,∠BCA=∠DCE=90°,且点D在线段AB上,连接AE.
(1)求证:①△BCD≌△ACE;②∠DAE=90°;
(2)若AB=8,当点D在线段AB上什么位置时,四边形ADCE的周长最小?请说明并求出周长的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:
员工 | 管理人员 | 普通工作人员 | |||||
人员结构 | 总经理 | 部门经理 | 科研人员 | 销售人员 | 高级技工 | 中级技工 | 勤杂工 |
员工数(名) | 1 | 3 | 2 | 3 | 24 | 1 | |
每人月工资(元) | 21000 | 8400 | 2025 | 2200 | 1800 | 1600 | 950 |
请你根据上述内容,解答下列问题:
(1)该公司“高级技工”有 名;
(2)所有员工月工资的平均数x为2500元,中位数为 元,众数为 元;
(3)小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;
(4)去掉四个管理人员的工资后,请你计算出其他员工的月平均工资![]() (结果保留整数),并判断
(结果保留整数),并判断![]() 能否反映该公司员工的月工资实际水平.
能否反映该公司员工的月工资实际水平.

查看答案和解析>>
科目:初中数学 来源: 题型:
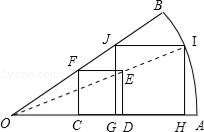
【题目】小明手上一张扇形纸片OAB.现要求在纸片上截一个正方形,使它的面积尽可能大.
小明的方案是:如图,在扇形纸片OAB内,画正方形CDEF,使C、D在OA上,F在OB上;连接OE并延长交弧AB于I,画IH∥ED交OA于H,IJ∥OA交OB于J,再画JG∥FC交OA于G.
(1)你认为小明画出的四边形GHIJ是正方形吗?如果是,请证明.如果不是,请说明理由.
(2)如果扇形OAB的圆心角∠AOB=30°,OA=6cm,小明截得的四边形GHIJ面积是多少(结果精确到0.1cm).
(3)(1)中小明画出的四边形GHIJ如果是正方形,我们把它叫做扇形的内接正方形(四个顶点分别在扇形的半径和弧上).请你再画出一种不同于图(1)的扇形的内接正方形(保留画图痕迹,不要求证明)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
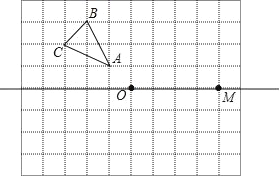
【题目】如图,它是一个8×10的网格,每个小正方形的边长均为1,每个小正方形的顶点叫格点,△ABC的顶点均在格点上.
(1)画出△ABC关于直线OM对称的△A1B1C1.
(2)画出△ABC关于点O的中心对称图形△A2B2C2.
(3)△A1B1C1与△A2B2C2组成的图形是轴对称图形吗?如果是,请画出对称轴.△A1B1C1与△A2B2C2组成的图形 (填“是”或“不是”)轴对称图形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com