
【题目】(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.

【答案】结论:(1)60;(2)AD=BE;应用:∠AEB=90°;AE=2CM+BE;
【解析】
试题探究:(1)通过证明△CDA≌△CEB,得到∠CEB=∠CDA=120°,又∠CED=60°,∴∠AEB=120°- 60°= 60°;
(2)已证△CDA≌△CEB,根据全等三角形的性质可得AD=BE;
应用:通过证明△ACD≌△BCE,得到AD = BE,∠BEC = ∠ADC=135°,所以∠AEB =∠BEC-∠CED =135°- 45°= 90°;根据等腰直角三角形的性质可得DE = 2CM,所以AE = DE+AD=2CM+BE.
试题解析:解:探究:(1)在△CDA≌△CEB中,
AC=BC,∠ACD=∠BCE,CD=CE,
∴△CDA≌△CEB,
∴∠CEB=∠CDA=120°,
又∠CED=60°,
∴∠AEB=120°- 60°= 60°;
(2)∵△CDA≌△CEB,
∴AD=BE;
应用:∠AEB=90°;AE=2CM+BE;
理由:∵△ACB和△DCE均为等腰直角三角形,∠ACB =∠DCE= 90°,
∴AC = BC, CD = CE, ∠ACB =∠DCB =∠DCE-∠DCB, 即∠ACD = ∠BCE,
∴△ACD≌△BCE,
∴AD = BE,∠BEC = ∠ADC=135°.
∴∠AEB =∠BEC-∠CED =135°- 45°= 90°.
在等腰直角三角形DCE中,CM为斜边DE上的高,
∴CM =" DM" = ME,∴DE = 2CM.
∴AE = DE+AD=2CM+BE.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】父亲两次将100斤粮食分给兄弟俩,第一次分给哥哥的粮食等于第二次分给弟弟的2倍,第二次分给哥哥的粮食是第一次分给弟弟的3倍,求两次分粮食中,哥哥、弟弟各分到多少粮食?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边上一点,连接BD,点
边上一点,连接BD,点![]() 为
为![]() 上一点,连接
上一点,连接![]() ,
,![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,交
,交![]() 于点
于点![]() .
.
(1)求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 为
为![]() 的中点,求证:
的中点,求证:![]() ;
;
(3)在(2)的条件下,如图3,若![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
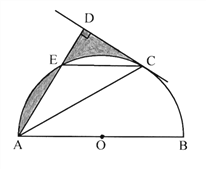
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD![]() CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
CD,垂足为D,AD交⊙O 于E,连接CE.(1)求证:CD 是⊙O 的切线
(2)若E是弧AC的中点,⊙O 的半径为1,求图中阴影部分的面积。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高校共有5个大餐厅和2个小餐厅。经过测试:同时开放1个大餐厅和2个小餐厅,可供1680名学生就餐;同时开放2个大餐厅和1个小餐厅,可供2280名学生就餐。
(1)1个大餐厅和1个小餐厅分别可供多少名学生就餐?
(2)若7个餐厅同时开放,能否供全校的5300名学生就餐?请说明理由
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在离水面高度为5m的岸上有人用绳子拉船靠岸,开始绳子与水面的夹角为30°,此人以每秒0.5m的速度收绳.
(1)8秒后船向岸边移动了多少米?
(2)写出还没收的绳子的长度S米与收绳时间t秒的函数关系式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y=ax2+bx+c的图象如图所示,其对称轴为直线x=-1,与x轴的一个交点为(1,0),与y轴的交点在(0,2)与(0,3)之间(不包含端点),有如下结论:①.2a+b=0 ②. 3a+2c<0 ③.a+5b+2c>0;④.-1<a<-![]() ,则结论正确的有_____________.
,则结论正确的有_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在△ABC的边AC上,要判断△ADB与△ABC相似,添加一个条件,不正确的是( )
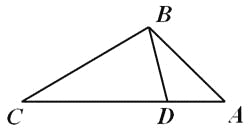
A.∠ABD=∠CB.∠ADB=∠ABCC.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:已知∠A=∠F,∠C=∠D,试说明:BD∥CE.
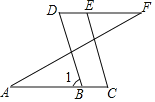
解:∵∠A=∠F(已知)
∴AC∥DF(______)
∴∠D=∠1(______)
又∵∠C=∠D(已知)
∴∠1=______
∴BD∥CE(______)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com