【题目】如图(图①为实景侧视图,图②为安装示意图),在屋顶的斜坡面上安装太阳能热水器:先安装支架AB和CD(均与水平面垂直),再将集热板安装在AD上.为使集热板吸热率更高,公司规定:AD与水平线夹角为θ1,且在水平线上的射影AF为1.4 m.现已测量出屋顶斜面与水平面夹角为θ2,并已知tan θ1=1.082,tan θ2=0.412.如果安装工人已确定支架AB高为25 cm,求支架CD的高.(结果精确到1 cm)
【答案】119cm.
【解析】试题分析：过点A作AE∥BC,交CD于点E,作BG∥AF交DF的延长线于点G. 则∠EAF=θ2, EC=AB=25 cm.再根据锐角三角函数的定义用
表示出
的值，再根据
进行解答即可．
试题解析：如图,过点A作AE∥BC,交CD于点E,作BG∥AF交DF的延长线于点G.
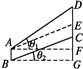
则∠EAF=∠CBG=θ2,且EC=AB=25 cm.
在Rt△DAF中,∠DAF=θ1,DF=AFtan θ1.
在Rt△EAF中,∠EAF=θ2,EF=AFtan θ2,
DE=DF-EF=AF(tan θ1-tan θ2).
AF=140 cm,tan θ1=1.082,tan θ2=0.412,
DE=140×(1.082-0.412)=93.8 (cm),
DC=DE+EC=93.8+25=118.8≈119(cm).
答:支架DC的高约为119 cm.
科目：初中数学 来源： 题型：
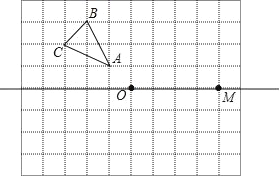
【题目】如图，它是一个8×10的网格，每个小正方形的边长均为1，每个小正方形的顶点叫格点，△ABC的顶点均在格点上．
（1）画出△ABC关于直线OM对称的△A1B1C1．
（2）画出△ABC关于点O的中心对称图形△A2B2C2．
（3）△A1B1C1与△A2B2C2组成的图形是轴对称图形吗？如果是，请画出对称轴．△A1B1C1与△A2B2C2组成的图形 （填“是”或“不是”）轴对称图形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：BC∥OA，∠B=∠A=120°，试回答下列问题：
(1)如图1所示，求证：OB∥AC；
(2)如图2，若点E、F在BC上，且满足∠FOC=∠AOC，并且OE平分∠BOF，则∠EOC的度数是______；
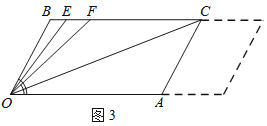
(3)在(2)的条件下，若平行移动AC，其它条件不变，如图3，则∠OCB：∠OFB的值是______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，点A（﹣3，0），点B是x轴上异于点A一动点，设B（x，0），以AB为边在x轴的上方作正方形ABCD．
（1）如图（1），若点B（1，0），则点D的坐标为 ；
（2）若点E是AB的中点，∠DEF＝90°，且EF交正方形外角的平分线BF于F．
①如图（2），当x＞0时，求证：DE＝EF；
②若点F的纵坐标为y，求y关于x的函数解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某中学为了了解学生每天完成家庭作业所用时间的情况，从每班抽取相同数量的学生进行调查，并将所得数据进行整理，制成条形统计图和扇形统计图，如图所示：
(1)补全条形统计图；
(2)求扇形统计图中扇形D的圆心角的度数；
(3)若该中学有2000名学生，请估计其中有多少名学生能在1.5 h内完成家庭作业．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC是等边三角形,点A与点D的坐标分别是A(4,0),D(10,0).
(1)如图①,当点C与点O重合时,求直线BD的表达式;
(2)如图②,点C从点O沿y轴向下移动,当以点B为圆心,AB为半径的☉B与y轴相切(切点为C)时,求点B的坐标;
(3)如图③,点C从点O沿y轴向下移动,当点C的坐标为C(0,-2
)时,求∠ODB的正切值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在⊙O中，AB是⊙O的直径，AB=10， 
，点E是点D关于AB的对称点，M是AB上的一动点，下列结论：①∠BOE=60°；②∠CED=
∠AOD；③DM⊥CE；④CM+DM的最小值是10，其中正确的序号是______．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在Rt△ABC中，∠BCA＝90°，∠A＜∠ABC，D是AC边上一点，且DA＝DB，O是AB的中点，CE是△BCD的中线．
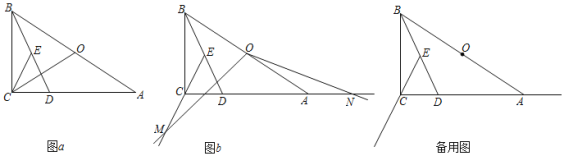
(1)如图a，连接OC，请直接写出∠OCE和∠OAC的数量关系： ；
(2)点M是射线EC上的一个动点，将射线OM绕点O逆时针旋转得射线ON，使∠MON＝∠ADB，ON与射线CA交于点N．
①如图b，猜想并证明线段OM和线段ON之间的数量关系；
②若∠BAC＝30°，BC＝m，当∠AON＝15°时，请直接写出线段ME的长度(用含m的代数式表示)．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司为奖励在趣味运动会上取得好成绩的员工，计划购买甲、乙两种奖品共20件，其中甲种奖品每件40元，乙种奖品每件30元．
（1）如果购买甲、乙两种奖品共花费了650元，求甲、乙两种奖品各购买了多少件；
（2）如果购买乙种奖品的件数不超过甲种奖品件数的2倍，总花费不超过680元，求该公司有哪几种不同的购买方案．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com