练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】等边三角形ABC 中，BD是角平分线，点E在BC边的延长线上，且CD=CE，则∠BDE的度数是（ ）

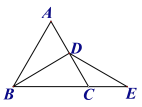
    A.90°B.100°C.120°D.无法确定

    【答案】C

    【解析】

    根据等边三角形的性质可得∠ACB=60°，∠DBC=30°，根据CD=CE可得∠CDE=∠CED，根据∠CDE+∠CED=∠ACB即可求得∠CED=30°．进而可得到∠BDE的度数.

    解：∵三角形ABC是等边三角形，BD是角平分线，

    ∴∠ACB=60°，∠DBC=∠ABC= 30°，

    ∵CD=CE，

    ∴∠CDE=∠CED，

    ∵∠CDE+∠CED=∠ACB

    ∴∠CED=30°，

    ∴∠BDE=180°-∠DBC-∠CED

    =180°-30°-30°

    =120°

    故选：C

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，△ABC中，AC的垂直平分线DE与∠ABC的角平分线相交于点D，垂足为点E，若∠ABC=72°，求∠ADC的度数.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知，如图，在等腰直角△ABC中，∠C=90°，AC=BC=4,点D是BC上一点，CD=1，点P是AB边上一动点，则PC+PD的最小值是________．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】请回答下列问题：

    （1）2317000用科学记数法表示是_______．

    （2）2.5678精确到百分位的近似数是________．

    （3）近似数精确到_______位．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC中，AB=AC，D是BC的中点，以AC为腰向外作等腰直角△ACE，∠EAC=90°，连接BE，交AD于点F，交AC于点G．

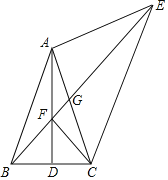
    （1）若∠BAC=50°，求∠AEB的度数；

    （2）求证：∠AEB=∠ACF；

    （3）试判断线段EF、BF与AC三者之间的等量关系，并证明你的结论．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

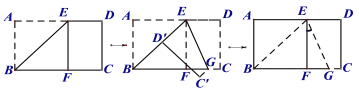
    【题目】将长方形纸片ABCD沿过点B的直线折叠，使点A落在BC边上点F处，折痕为BE，再沿过点E的直线折叠，使点D落在BE边上点D’处，折痕为EG，展平纸片，则图中∠FEG= ______ °

    查看答案和解析>>

    科目：初中数学 来源： 题型：

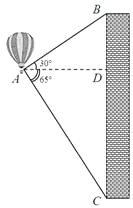
    【题目】（6分）如图，热气球的探测器显示，从热气球A处看一栋高楼顶部B的仰角为30°，看这栋高楼底部C的俯角为65°，热气球与高楼的水平距离AD为120m．求这栋高楼的高度．（结果用含非特殊角的三角函数及根式表示即可）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明同学在数学实践课中测量路灯的高度．如图，已知他的目高为1.5米，他先站在处看路灯顶端的仰角为，向前走3米后站在处，此时看灯顶端的仰角为（），则灯顶端到地面的距离约为（ ）

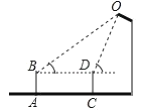
    A.3.2米B.4.1米C.4.7米D.5.4米

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（　　）

    A. 15 B. 18 C. 21 D. 24

    查看答案和解析>>

    同步练习册答案