
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
科目:初中数学 来源: 题型:
【题目】如图,线段AC=6,线段BC=15,点M是AC的中点,在CB上取一点N,使得CN:NB=1:2,求MN的长.
解:∵M是AC的中点,AC=6,
∴MC=![]() ______(填线段名称)=______,
______(填线段名称)=______,
又因为CN:NB=1:2,BC=15,
∴CN=![]() ______(填线段名称)=______.
______(填线段名称)=______.
∴MN=______(填线段名称)+______(填线段名称)=8
∴MN的长为8.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有2部不同的电影A、B,甲、乙、丙3人分别从中任意选择1部观看.
(1)求甲选择A部电影的概率;
(2)求甲、乙、丙3人选择同一部电影的概率(请用画树状图的方法给出分析过程,并求出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD平分∠ABC交AC于点D,AE∥BD交CB的延长线于点E.若∠E=35°,则∠BAC的度数为( )

A. 40° B. 45° C. 60° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形纸片ABC中,点D在边AB(不包含端点A、B)上运动,连接CD,将∠ADC对折,点A落在直线CD上的点A′处,得到折痕DE;将∠BDC对折,点B落在直线CD上的点B′处,得到折痕DF.
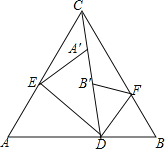
(1)若∠ADC=80°,求∠BDF的度数;
(2)试问∠EDF的大小是否会随着点D的运动而变化?若不变,求出∠EDF的大小;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,CN是等边△ABC的外角∠ACM内部的一条射线,点A关于CN的对称点为D,连接AD,BD,CD,其中AD,BD分别交射线CN于点E,P.
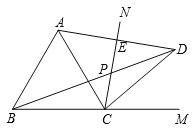
(1)求证:CD=CB;
(2)若∠ACN= a,求∠BDC的大小(用含a的式子表示);
(3)请判断线段PB,PC与PE三者之间的数量关系,并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不含B、C两点),将 ![]() ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将
ABP沿直线AP翻折,点B落在点E处;在CD上有一点M,使得将 ![]() CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).
CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接MA,NA.则以下结论中正确的个数有( ).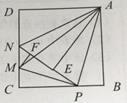
① ![]() CMP∽
CMP∽ ![]() BPA;
BPA;
②四边形AMCB的面积最大值为10;
③当P为BC中点时,AE为线段NP的中垂线;
④线段AM的最小值为2 ![]() ;
;
⑤当 ![]() ABP≌
ABP≌ ![]() AND时,BP=4
AND时,BP=4 ![]() -4.
-4.
A.①②③
B.②③⑤
C.①④⑤
D.①②⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.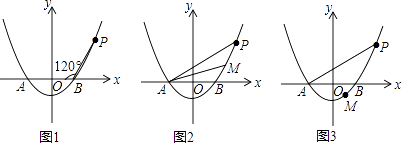
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为 ![]() ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com