
【题目】已知抛物线y=ax2﹣4a(a>0)与x轴相交于A,B两点(点A在点B的左侧),点P是抛物线上一点,且PB=AB,∠PBA=120°,如图所示.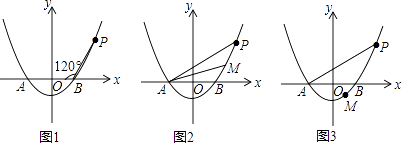
(1)求抛物线的解析式.
(2)设点M(m,n)为抛物线上的一个动点,且在曲线PA上移动.
①当点M在曲线PB之间(含端点)移动时,是否存在点M使△APM的面积为 ![]() ?若存在,求点M的坐标;若不存在,请说明理由.
?若存在,求点M的坐标;若不存在,请说明理由.
②当点M在曲线BA之间(含端点)移动时,求|m|+|n|的最大值及取得最大值时点M的坐标.
【答案】
(1)解:如图1, 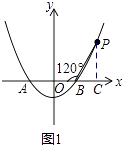
令y=0代入y=ax2﹣4a,
∴0=ax2﹣4a,
∵a>0,
∴x2﹣4=0,
∴x=±2,
∴A(﹣2,0),B(2,0),
∴AB=4,
过点P作PC⊥x轴于点C,
∴∠PBC=180°﹣∠PBA=60°,
∵PB=AB=4,
∴cos∠PBC= ![]() ,
,
∴BC=2,
由勾股定理可求得:PC=2 ![]() ,
,
∵OC=OB+BC=4,
∴P(4,2 ![]() ),
),
把P(4,2 ![]() )代入y=ax2﹣4a,
)代入y=ax2﹣4a,
∴2 ![]() =16a﹣4a,
=16a﹣4a,
∴a= ![]() ,
,
∴抛物线解析式为;y= ![]() x2﹣
x2﹣ ![]() ;
;
(2)解:∵点M在抛物线上,
∴n= ![]() m2﹣
m2﹣ ![]() ,
,
∴M的坐标为(m, ![]() m2﹣
m2﹣ ![]() ),
),
①当点M在曲线PB之间(含端点)移动时,
∴2≤m≤4,
如图2,过点M作ME⊥x轴于点E,交AP于点D, 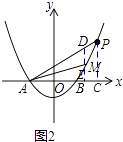
设直线AP的解析式为y=kx+b,
把A(﹣2,0)与P(4,2 ![]() )代入y=kx+b,
)代入y=kx+b,
得: ![]() ,
,
解得 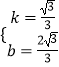
∴直线AP的解析式为:y= ![]() x+
x+ ![]() ,
,
令x=m代入y= ![]() x+
x+ ![]() ,
,
∴y= ![]() m+
m+ ![]() ,
,
∴D的坐标为(m, ![]() m+
m+ ![]() ),
),
∴DM=( ![]() m+
m+ ![]() )﹣(
)﹣( ![]() m2﹣
m2﹣ ![]() )=﹣
)=﹣ ![]() m2+
m2+ ![]() m+
m+ ![]() ,
,
∴S△APM= ![]() DMAE+
DMAE+ ![]() DMCE
DMCE
= ![]() DM(AE+CE)
DM(AE+CE)
= ![]() DMAC
DMAC
=﹣ ![]() m2+
m2+ ![]() m+4
m+4 ![]()
当S△APM= ![]() 时,
时,
∴ ![]() =﹣
=﹣ ![]() m2+
m2+ ![]() m+4
m+4 ![]() ,
,
∴解得m=3或m=﹣1,
∵2≤m≤4,
∴m=3,
此时,M的坐标为(3, ![]() );
);
②当点M在曲线BA之间(含端点)移动时,
∴﹣2≤m≤2,n<0,
当﹣2≤m≤0时,
∴|m|+|n|=﹣m﹣n=﹣ ![]() m2﹣m+
m2﹣m+ ![]() =﹣
=﹣ ![]() (m+
(m+ ![]() )2+
)2+ ![]() ,
,
当m=﹣ ![]() 时,
时,
∴|m|+|n|可取得最大值,最大值为 ![]() ,
,
此时,M的坐标为(﹣ ![]() ,﹣
,﹣ ![]() ),
),
当0<m≤2时,
∴|m|+|n|=m﹣n=﹣ ![]() m2+m+
m2+m+ ![]() =﹣
=﹣ ![]() (m﹣
(m﹣ ![]() )2+
)2+ ![]() ,
,
当m= ![]() 时,
时,
∴|m|+|n|可取得最大值,最大值为 ![]() ,
,
此时,M的坐标为( ![]() ,﹣
,﹣ ![]() ),
),
综上所述,当点M在曲线BA之间(含端点)移动时,M的坐标为( ![]() ,﹣
,﹣ ![]() )或(﹣
)或(﹣ ![]() ,﹣
,﹣ ![]() )时,|m|+|n|的最大值为
)时,|m|+|n|的最大值为 ![]() .
.
【解析】(1)首先令y=0得到关于x的方程,从而可求出A、B两点坐标,然后过点P作PC⊥x轴于点C,接下来,根据∠PBA=120°,PB=AB,分别求出BC和PC的长度即可得出点P的坐标,最后将点P的坐标代入二次函数解析式即;
(2)①过点M作ME⊥x轴于点E,交AP于点D,分别用含m的式子表示点D、M的坐标,然后代入△APM的面积公式![]() DMAC,根据题意列出方程求出m的值;②根据题意可知:n<0,然后对m的值进行分类讨论,当-2≤m≤0时,|m|=-m;当0<m≤2时,|m|=m,列出函数关系式即可求得|m|+|n|的最大值
DMAC,根据题意列出方程求出m的值;②根据题意可知:n<0,然后对m的值进行分类讨论,当-2≤m≤0时,|m|=-m;当0<m≤2时,|m|=m,列出函数关系式即可求得|m|+|n|的最大值


科目:初中数学 来源: 题型:
【题目】如图,圆柱底面半径为![]() cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
cm,高为9cm,点A、B分别是圆柱两底面圆周上的点,且A、B在同一母线上,用一根棉线从A点顺着圆柱侧面绕3圈到B点,则这根棉线的长度最短为( )
A. 12cm B. ![]() cm C. 15cm D.
cm C. 15cm D. ![]() cm
cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,ABCD的周长为36,对角线AC、BD相交于点O,点E是CD的中点,BD=12,则△DOE的周长为( )

A. 15 B. 18 C. 21 D. 24
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O是正△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:①△BO′A可以由△BOC绕点B逆时针旋转60°得到;②点O与O′的距离为4;③∠AOB=150°;④S四边形AOBO′=6+3![]() ;其中正确的结论是( )
;其中正确的结论是( )

A. ①②③ B. ①③④ C. ②③④ D. ①②
查看答案和解析>>
科目:初中数学 来源: 题型:
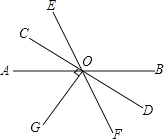
【题目】如图,直线AB、CD、EF相交于点O,OG⊥CD,∠BOD=32°.
(1)求∠AOG的度数;
(2)如果OC是∠AOE的平分线,那么OG是∠AOF的平分线吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
(1) 请画出△ABC向左平移5个单位长度后得到的△A![]() B
B![]() C
C![]() ;
;
(2) 请画出△ABC关于原点对称的△A![]() B
B![]() C
C![]() ;
;
(3) 在![]() 轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.
轴上求作一点P,使△PAB的周长最小,请画出△PAB,并直接写出P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC与△A′B′C′中,有下列条件:(1) ![]() ,(2)
,(2) ![]() ;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
;(3)∠A=∠A′;(4)∠C=∠C′,如果从中任取两个条件组成一组,那么能判断△ABC∽△A′B′C′的共有( )
A.1组
B.2组
C.3组
D.4组
查看答案和解析>>
科目:初中数学 来源: 题型:
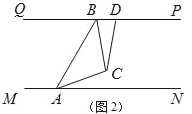
【题目】“一带一路”让中国和世界更紧密,“中欧铁路”为了安全起见在某段铁路两旁安置了两座可旋转探照灯.如图1所示,灯A射线从AM开始顺时针旋转至AN便立即回转,灯B射线从BP开始顺时针旋转至BQ便立即回转,两灯不停交叉照射巡视.若灯A转动的速度是每秒2度,灯B转动的速度是每秒1度.假定主道路是平行的,即PQ∥MN,且∠BAM:∠BAN=2:1.
(1)填空:∠BAN=_____°;
(2)若灯B射线先转动30秒,灯A射线才开始转动,在灯B射线到达BQ之前,A灯转动几秒,两灯的光束互相平行?
(3)如图2,若两灯同时转动,在灯A射线到达AN之前.若射出的光束交于点C,过C作∠ACD交PQ于点D,且∠ACD=120°,则在转动过程中,请探究∠BAC与∠BCD的数量关系是否发生变化?若不变,请求出其数量关系;若改变,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com