练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在△ABC中，AB=AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E．若∠E=35°，则∠BAC的度数为（ ）

    A. 40° B. 45° C. 60° D. 70°

    【答案】A

    【解析】

    根据平行线的性质可得∠CBD的度数，根据角平分线的性质可得∠CBA的度数，根据等腰三角形的性质可得∠C的度数，根据三角形内角和定理可得∠BAC的度数．

    解：∵AE∥BD，∴∠CBD=∠E=35°，∵BD平分∠ABC，∴∠CBA=70°，∵AB=AC，

    ∴∠C=∠CBA=70°，∴∠BAC=180°﹣70°×2=40°．

    故选A．

    “点睛”考查了平行线的性质，角平分线的性质，等腰三角形的性质和三角形内角和定理．关键是得到∠C=∠CBA=70°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图，已知：E是∠AOB的平分线上一点，EC⊥OB，ED⊥OA，C、D是垂足，连接CD，且交OE于点F.

    （1）求证：OE是CD的垂直平分线.

    （2）若∠AOB=60，请你探究OE，EF之间有什么数量关系？并证明你的结论。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，圆柱底面半径为cm，高为9cm，点A、B分别是圆柱两底面圆周上的点，且A、B在同一母线上，用一根棉线从A点顺着圆柱侧面绕3圈到B点，则这根棉线的长度最短为（ ）

    A. 12cm B. cm C. 15cm D. cm

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知函数的图像与轴交于点，一次函数的图像分别与轴、轴交于点，且与的图像交于点.

    (1)求的值;

    (2)若，则的取值范围是 ；

    (3)求四边形的面积.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

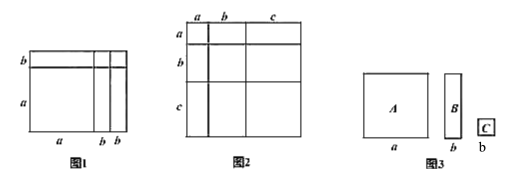
    【题目】我们知道:有些代数恒等式可以利用平面图形的面积来表示，如：

    就可以用如图所示的面积关系来说明。

    (1)请根据如图写出代数恒等式,并根据所写恒等式计算：

    (2)若求的值；

    (3)现有如图中的彩色卡片:A型、B型、C型，把这些卡片不重叠不留缝隙地贴在棱长为的100个立方体表面进行装饰，A型、B型、C型卡片的单价分别为0.7元/张、0.5元/张、0.4元/张，共需多少费用?

    查看答案和解析>>

    科目：初中数学 来源： 题型：

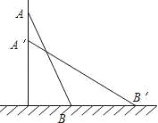
    【题目】如图，一架梯子AB长13米，斜靠在一面墙上，梯子底端离墙5米.（1）这个梯子的顶端距地面有多高？（2）如果梯子的顶端下滑了5米，那么梯子的底端在水平方向滑动了多少米？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，ABCD的周长为36，对角线AC、BD相交于点O，点E是CD的中点，BD=12，则△DOE的周长为（　　）

    A. 15 B. 18 C. 21 D. 24

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，O是正△ABC内一点，OA＝3，OB＝4，OC＝5，将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′，下列结论：①△BO′A可以由△BOC绕点B逆时针旋转60°得到；②点O与O′的距离为4；③∠AOB＝150°；④S四边形AOBO′＝6+3；其中正确的结论是(　　)

    A. ①②③ B. ①③④ C. ②③④ D. ①②

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图△ABC中，D、E是AB、AC上点，AB=7.8，AD=3，AC=6，AE=3.9，试判断△ADE与△ABC是否会相似．

    查看答案和解析>>

    同步练习册答案