
【题目】如图,正方形![]() 的边长为
的边长为![]() ,
,![]() 在正方形外,
在正方形外,![]() ,过
,过![]() 作
作![]() 于
于![]() ,直线
,直线![]() ,
,![]() 交于点
交于点![]() ,直线
,直线![]() 交直线
交直线![]() 于点
于点![]() ,则下列结论正确的是( )
,则下列结论正确的是( )

①![]() ;②
;②![]() ;③
;③![]() ;
;
④若![]() ,则
,则![]()
A.1个B.2个C.3个D.4个
【答案】C
【解析】
①利用等腰三角形的性质即可证明.②根据DA=DC=DE,利用圆周角定理可知∠AEC=![]() ∠ADC=45°,即可解决问题.③如图,作DF⊥DM交PM于F,证明△ADM≌△CDF(SAS)即可解决问题.④解直角三角形求出CE=EF=
∠ADC=45°,即可解决问题.③如图,作DF⊥DM交PM于F,证明△ADM≌△CDF(SAS)即可解决问题.④解直角三角形求出CE=EF=![]() 可得结论.
可得结论.
∵四边形ABCD是正方形,
∴DA=DC,∠ADC=90°,
∵DC=DE,
∴DA=DE,
∴∠DAE=∠DEA,故①正确,
∵DA=DC=DE,
∴∠AEC=![]() ∠ADC=45°(圆周角定理),
∠ADC=45°(圆周角定理),
∵DM⊥AE,
∴∠EHM=90°,
∴∠DMC=45°,故②正确,
如图,作DF⊥DM交PM于F,
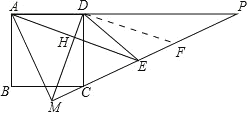
∵∠ADC=∠MDF=90°,
∴∠ADM=∠CDF,
∵∠DMF=45°,
∴∠DMF=∠DFM=45°,
∴DM=DF,∵DA=DC,
∴△ADM≌△CDF(SAS),
∴AM=CF,
∴AM+CM=CF+CM=MF=![]() DM,
DM,
∴![]() =
=![]() ,故③正确,
,故③正确,
若MH=2,则易知AH=MH=HE=2,AM=EM=2![]() ,
,
在Rt△ADH中, ![]() ,
,
∴DM=3,AM+CM=3![]() ,
,
∴CM=CE=![]() ,
,
∴S△DCM=S△DCE,故④错误,
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】请解答下列各题:
(1)数轴上表示![]() 和
和![]() 的两点
的两点![]() 和
和![]() 之间的距离表示为_______,如果
之间的距离表示为_______,如果![]() ,那么
,那么![]() _______.
_______.
(2)若点![]() 表示的整数为
表示的整数为![]() ,则当
,则当![]() ________时,
________时,![]() .
.
(3)要使![]() 取最小值时,相应的
取最小值时,相应的![]() 的取值范围是________,最小值是________.
的取值范围是________,最小值是________.
(4)已知![]() ,则
,则![]() 的最大值为_______,最小值为_______.
的最大值为_______,最小值为_______.
(5)若![]() ,则
,则![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图22,将—矩形OABC放在直角坐际系中,O为坐标原点.点A在x轴正半轴上.点E是边AB上的—个动点(不与点A、N重合),过点E的反比例函数![]() 的图象与边BC交于点F。
的图象与边BC交于点F。
【1】若△OAE、△OCF的而积分别为S1、S2.且S1+S2=2,求![]() 的值:
的值:
【2】若OA=2.0C=4.问当点E运动到什么位置时,四边形OAEF的面积最大.其最大值为多少?
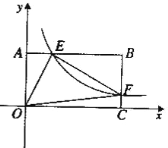
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有![]() 、
、![]() 两种商品,已知买一件
两种商品,已知买一件![]() 商品要比买一件
商品要比买一件![]() 商品少30元,用160元全部购买
商品少30元,用160元全部购买![]() 商品的数量与用400元全部购买
商品的数量与用400元全部购买![]() 商品的数量相同.
商品的数量相同.
(1)求![]() 、
、![]() 两种商品每件各是多少元?
两种商品每件各是多少元?
(2)如果小亮准备购买![]() 、
、![]() 两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
两种商品共10件,总费用不超过380元,且不低于300元,则如何购买才能使总费用最低?最低费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为圆
为圆![]() 的直径,
的直径,![]() 为圆
为圆![]() 上一点,
上一点,![]() 为
为![]() 延长线一点,且
延长线一点,且![]() ,
,![]() 于点
于点![]() .
.
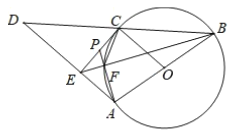
(1)求证:直线![]() 为圆
为圆![]() 的切线;
的切线;
(2)设![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,
,
①求证:![]()
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2+mx+n的图象经过点P(﹣3,1),对称轴是直线x=﹣1.
(1)求m,n的值;
(2)x取什么值时,y随x的增大而减小?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com