【题目】如图，抛物线
与
轴交于
、
两点，
是以点
（0,3）为圆心，2为半径的圆上的动点，
是线段
的中点，连结
.则线段的最大值是（ ）
A. 
B. 
C. 
D. 
阅读快车系列答案科目：初中数学 来源： 题型：
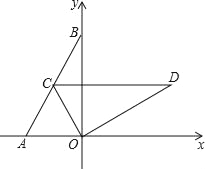
【题目】已知如图，在直角坐标系xOy中，点A，点B坐标分别为（﹣1，0），（0，
），连结AB，OD由△AOB绕O点顺时针旋转60°而得．
（1）求点C的坐标；
（2）△AOB绕点O顺时针旋转60°所扫过的面积；
（3）线段AB绕点O顺时针旋转60°所扫过的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
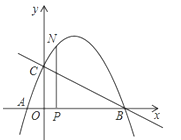
【题目】如图，抛物线与x轴交于点A（﹣
， 0），点B（2，0），与y轴交于点C（0，1），连接BC．
（1）求抛物线的解析式；
（2）N为抛物线上的一个动点，过点N作NP⊥x轴于点P，设点N的横坐标为t（﹣＜t＜2），求△ABN的面积s与t的函数解析式；
（3）若0＜t＜2且t≠0时，△OPN∽△COB，求点N的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在平面直角坐标系中，直线y=﹣4x+4与x轴、y轴分别交于A．B两点，以AB为边在第一象限内作正方形ABCD，顶点D在双曲线y=kx-1上，将该正方形沿x轴负方向平移a个单位长度后，顶点C恰好落在双曲线y=kx-1上，则a的值是（ ）
A. 3 B. 4 C. 5 D. 6
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】观察下列等式：
（a﹣b）（a+b）＝a2﹣b2
（a﹣b）（a2+ab+b2）＝a3﹣b3
（a﹣b）（a3+a2b+ab2+b3）＝a4﹣b4…
利用你的发现的规律解决下列问题
（1）（a﹣b）（a4+a3b+a2b2+ab3+b4）＝ （直接填空）；
（2）（a﹣b）（an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1）＝ （直接填空）；
（3）利用（2）中得出的结论求62019+62018+…+62+6+1的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形
的边长为
，
在正方形外，
，过
作
于
，直线
，
交于点
，直线
交直线
于点
，则下列结论正确的是（ ）
①
；②
；③
；
④若
，则
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读理解：
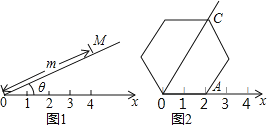
如图1，在平面内选一定点O，引一条有方向的射线Ox，再选定一个单位长度，那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定，有序数对（θ，m）称为M点的“极坐标”，这样建立的坐标系称为“极坐标系”．
应用：在图2的极坐标系下，如果正六边形的边长为2，有一边OA在射线Ox上，则正六边形的顶点C的极坐标应记为（ ）
A．（60°，4） B．（45°，4） C．（60°，2
） D．（50°，2 ）
查看答案和解析>>
科目：初中数学 来源： 题型：
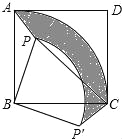
【题目】已知，点P是正方形ABCD内的一点，连接PA，PB，PC．将△PAB绕点B顺时针旋转90°到△P′CB的位置（如图）．
（1）设AB的长为a，PB的长为b（b＜a），求△PAB旋转到△P′CB的过程中边PA所扫过区域（图中阴影部分）的面积；
（2）若PA=2，PB=4，∠APB=135°，求PC的长．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
