
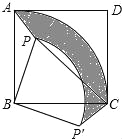
【题目】已知,点P是正方形ABCD内的一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图).
(1)设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图中阴影部分)的面积;
(2)若PA=2,PB=4,∠APB=135°,求PC的长.
【答案】(1)![]() (a2-b2);(2)6.
(a2-b2);(2)6.
【解析】
试题分析:(1)依题意,将△P′CB逆时针旋转90°可与△PAB重合,此时阴影部分面积=扇形BAC的面积-扇形BPP'的面积,根据旋转的性质可知,两个扇形的中心角都是90°,可据此求出阴影部分的面积.
(2)连接PP',根据旋转的性质可知:BP=BP',旋转角∠PBP'=90°,则△PBP'是等腰直角三角形,∠BP'C=∠BPA=135°,∠PP'C=∠BP'C-∠BP'P=135°-45°=90°,可推出△PP'C是直角三角形,进而可根据勾股定理求出PC的长.
试题解析:(1)∵将△PAB绕点B顺时针旋转90°到△P′CB的位置,
∴△PAB≌△P'CB,
∴S△PAB=S△P'CB,
S阴影=S扇形BAC-S扇形BPP′=![]() (a2-b2);
(a2-b2);
(2)连接PP′,根据旋转的性质可知:△APB≌△CP′B,
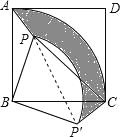
∴BP=BP′=4,P′C=PA=2,∠PBP′=90°,
∴△PBP'是等腰直角三角形,P'P2=PB2+P'B2=32;
又∵∠BP′C=∠BPA=135°,
∴∠PP′C=∠BP′C-∠BP′P=135°-45°=90°,即△PP′C是直角三角形.
PC=![]() =6.
=6.


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
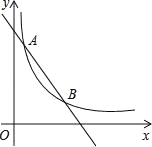
【题目】如图,一次函数y=-x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着人民生活水平的不断提高,滨州市家庭轿车的拥有量逐年增加,据统计,家景园小区2014年底拥有家庭轿车144辆,2016年底家庭轿车的拥有量达到225辆.
(1)若该小区2014年底到2016年底家庭轿车拥有量的年平均增长率都相同,求该小区到2017年底家庭轿车估计将达到多少辆?
(2)为了缓解停车矛盾,该小区决定2017年投资880万元建造若干个停车位,据测算,建造费用分别为室内车位60000元/个,露天车位20000元/个,考虑到实际因素,计划露天车位的数量是室内车位的2倍,那么该小区2017年底车位个数能否满足小区住户的停车需求?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象经过点A(1,0),B(2,0),C(0,-2),直线x=m(m>2)与x轴交于点D.
(1)求二次函数的解析式;
(2)在直线x=m(m>2)上有一点E(点E在第四象限),使得E、D、B为顶点的三角形与以A、O、C为顶点的三角形相似,求E点坐标(用含m的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com