
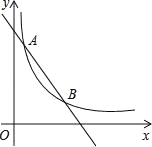
【题目】如图,一次函数y=-x+4的图象与反比例函数y=![]() (k为常数,且k≠0)的图象交于A(1,a),B两点.
(k为常数,且k≠0)的图象交于A(1,a),B两点.
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
【答案】(1)y=![]() ,点B的坐标为(3,1).(2)点P的坐标为(
,点B的坐标为(3,1).(2)点P的坐标为(![]() ,0).
,0).![]() .
.
【解析】
试题分析:(1)由点A在一次函数图象上,结合一次函数解析式可求出点A的坐标,再由点A的坐标利用待定系数法即可求出反比例函数解析式,联立两函数解析式成方程组,解方程组即可求出点B坐标;
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,连接PB.由点B、D的对称性结合点B的坐标找出点D的坐标,设直线AD的解析式为y=mx+n,结合点A、D的坐标利用待定系数法求出直线AD的解析式,令直线AD的解析式中y=0求出点P的坐标,再通过分割图形结合三角形的面积公式即可得出结论.
试题解析:(1)把点A(1,a)代入一次函数y=-x+4,
得:a=-1+4,解得:a=3,
∴点A的坐标为(1,3).
把点A(1,3)代入反比例函数y=![]() ,
,
得:3=k,
∴反比例函数的表达式y=![]() ,
,
联立两个函数关系式成方程组得: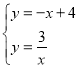 ,
,
解得:![]() ,或
,或![]() ,
,
∴点B的坐标为(3,1).
(2)作点B作关于x轴的对称点D,交x轴于点C,连接AD,交x轴于点P,此时PA+PB的值最小,连接PB,如图所示.
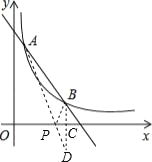
∵点B、D关于x轴对称,点B的坐标为(3,1),
∴点D的坐标为(3,- 1).
设直线AD的解析式为y=mx+n,
把A,D两点代入得:![]() ,
,
解得:![]() ,
,
∴直线AD的解析式为y=-2x+5.
令y=-2x+5中y=0,则-2x+5=0,
解得:x=![]() ,
,
∴点P的坐标为(![]() ,0).
,0).
S△PAB=S△ABD-S△PBD=![]() BD(xB-xA)-
BD(xB-xA)-![]() BD(xB-xP)
BD(xB-xP)
=![]() ×[1-(-1)]×(3-1)-
×[1-(-1)]×(3-1)-![]() ×[1-(-1)]×(3-
×[1-(-1)]×(3-![]() )
)
=![]() .
.


科目:初中数学 来源: 题型:
【题目】(本小题满分7分)完成下列各题:
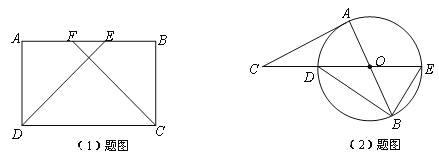
(1)如图,在矩形![]() 中,AF=BE. 求证:DE=CF;
中,AF=BE. 求证:DE=CF;
(2)如图,![]() 是
是![]() 的直径,
的直径,![]() 与
与![]() 相切于点A. 连接
相切于点A. 连接![]() 交
交![]() 于点
于点![]() ,
,![]() 的延长线交
的延长线交![]() 于点
于点![]() 连接
连接![]() ,
,![]() ,
,![]() 求
求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c与x轴交于A、B两点,顶点C的纵坐标为-2,现将抛物线向右平移2个单位,得到抛物线y=a1x2+b1x+c1,则下列结论正确的是 .(写出所有正确结论的序号)
①b>0
②a-b+c<0
③阴影部分的面积为4
④若c=-1,则b2=4a.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)(-8)× (-7)=______ (2)12×(-5)=______ (3)(-36)×(-1)=______ (4)(-25)×16=______ (5)100×(-0.001)=______ (6)-7.6×0.03=______
查看答案和解析>>
科目:初中数学 来源: 题型:
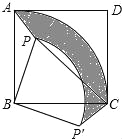
【题目】已知,点P是正方形ABCD内的一点,连接PA,PB,PC.将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图).
(1)设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图中阴影部分)的面积;
(2)若PA=2,PB=4,∠APB=135°,求PC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com