
【题目】阅读理解:
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
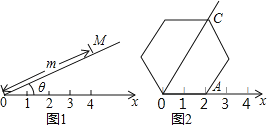
A.(60°,4) B.(45°,4) C.(60°,2![]() ) D.(50°,2
) D.(50°,2![]() )
)
科目:初中数学 来源: 题型:
【题目】股民王先生上周星期五买进某公司股票1000股,每股18元,本周该股票的涨跌情况如表(正数表示价格比前一天上涨,负数表示价格比前一天下跌,单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
(1)星期三结束时,该股票每股多少元?
(2)该股票本周内每股的最高价和最低价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决农村燃气困难,在P处建立了一个燃气站,从P站分别向A、B、C村铺设燃气管道。已知B村在A村的北偏东60°方向,距离A村2.4km,C村在A村的正东方向,距离A村1.8km,要使此工程费用最省,管道PA+PB+PC之和需最短,则最短长度为______________km.

查看答案和解析>>
科目:初中数学 来源: 题型:
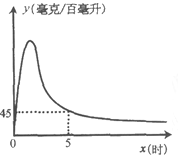
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为圆
为圆![]() 的直径,
的直径,![]() 为圆
为圆![]() 上一点,
上一点,![]() 为
为![]() 延长线一点,且
延长线一点,且![]() ,
,![]() 于点
于点![]() .
.
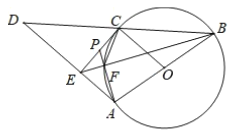
(1)求证:直线![]() 为圆
为圆![]() 的切线;
的切线;
(2)设![]() 与圆
与圆![]() 交于点
交于点![]() ,
,![]() 的延长线与
的延长线与![]() 交于点
交于点![]() ,
,
①求证:![]()
②若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE、CF分别是钝角△ABC(∠A>90°)的高,在BE上截取BP=AC,在CF的延长线截取CQ=AB,连结AP、AQ,请推测AP与AQ的数量和位置关系并加以证明。

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E是AB边的中点,沿EC对折矩形ABCD,使B点落在点P处,折痕为EC,连结AP并延长AP交CD于F点,连结CP并延长CP交AD于Q点.给出以下结论:
①四边形AECF为平行四边形;
②∠PBA=∠APQ;
③△FPC为等腰三角形;
④△APB≌△EPC.
其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.
(1)请再给出一种利用图象求方程x2-2x-1=0的解的方法;
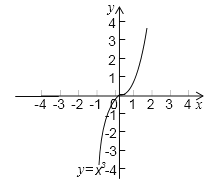
(2)已知函数y=x3的图象(如图),求方程x3-x-2=0的解(结果保留两位有效数字).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com