
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
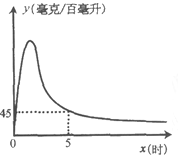
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
【答案】(1)①200;②225;(2)不能,理由见解析.
【解析】
试题(1)①根据二次函数的最值求解即可.
②根据点在曲线上点的坐标满足方程的关系,将(5,45)代入![]() 即可求得k的值.
即可求得k的值.
(2)求出![]() 时(即酒精含量等于20毫克/百毫升)对应的x值(所需时间),推出结论.
时(即酒精含量等于20毫克/百毫升)对应的x值(所需时间),推出结论.
试题解析:(1)①当![]() 时,
时,![]() ,
,
∴喝酒后1时血液中的酒精含量达到最大值,最大值为200毫克/百毫升.
②∵当![]() 时,
时,![]() ,且(5,45)在反比例函数
,且(5,45)在反比例函数![]() (k>0)图象上,
(k>0)图象上,
∴把(5,45)代入![]() 得
得![]() ,解得
,解得![]() .
.
(2)把![]() 代入反比例函数
代入反比例函数![]() 得
得![]() .
.
∴喝完酒经过11.25时(即11:20时)为早上7:20.
∴第二天早上7:20以后才可以驾驶,7:00时不能驾车去上班.


 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
【题目】如图,两条直线AB、CD相交于点O,且∠AOC=90°,射线OM从OB开始绕O点逆时针方向旋转,速度为15°/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12°/s.两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
(1)当t=2时,∠MON的度数为 ,∠BON的度数为 ;∠MOC的度数为
(2)当0<t<12时,若∠AOM=3∠AON-60°,试求出t的值;
(3)当0<t<6时,探究![]() 的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?

查看答案和解析>>
科目:初中数学 来源: 题型:
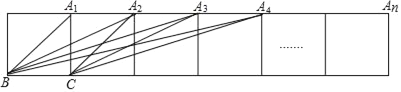
【题目】如图,把n个边长为1的正方形拼接成一排,求得tan∠BA1C=1,tan∠BA2C=![]() ,tan∠BA3C=
,tan∠BA3C=![]() ,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
,计算tan∠BA4C=_____,…按此规律,写出tan∠BAnC=_____(用含n的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列等式:
(a﹣b)(a+b)=a2﹣b2
(a﹣b)(a2+ab+b2)=a3﹣b3
(a﹣b)(a3+a2b+ab2+b3)=a4﹣b4…
利用你的发现的规律解决下列问题
(1)(a﹣b)(a4+a3b+a2b2+ab3+b4)= (直接填空);
(2)(a﹣b)(an﹣1+an﹣2b+an﹣3b2…+abn﹣2+bn﹣1)= (直接填空);
(3)利用(2)中得出的结论求62019+62018+…+62+6+1的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M.
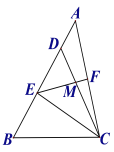
(1)求证:EF=![]() AC.
AC.
(2)连接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
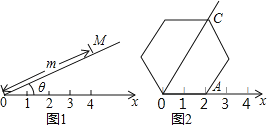
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
A.(60°,4) B.(45°,4) C.(60°,2![]() ) D.(50°,2
) D.(50°,2![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
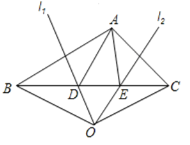
【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求![]() 的度数;
的度数;
(2)若BC=9,AC=12,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
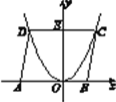
【题目】如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成ABCD,DC与y轴的交点为E(0,6),试求a的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com