
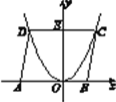
【题目】如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成ABCD,DC与y轴的交点为E(0,6),试求a的值.
科目:初中数学 来源: 题型:
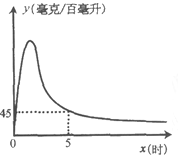
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
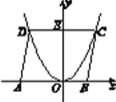
【题目】如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成ABCD,DC与y轴的交点为E(0,6),试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道:点A.B在数轴上分别表示有理数a、b,A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|a-b|.所以式子|x3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,解答下列问题:
![]()
(1)若|x3|=4,则x=______;
(2)式子|x3|=|x+1|,则x=______;
(3)若|x3|+|x+1|=9,借助数轴求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用图象解一元二次方程x2-2x-1=0时,我们采用的一种方法是在直角坐标系中画出抛物线y=x2和直线y=2x+1,两图象交点的横坐标就是该方程的解.
(1)请再给出一种利用图象求方程x2-2x-1=0的解的方法;
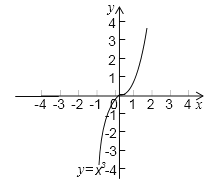
(2)已知函数y=x3的图象(如图),求方程x3-x-2=0的解(结果保留两位有效数字).
查看答案和解析>>
科目:初中数学 来源: 题型:
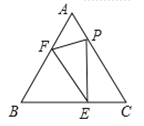
【题目】如图,等边![]() 的边长为
的边长为![]() ,
,![]() 是边
是边![]() 上的动点,
上的动点,![]() 交边
交边![]() 于点
于点![]() ,在边
,在边![]() 上取一点
上取一点![]() ,使
,使![]() ,连接
,连接![]() .
.
(1)请直接写出图中与线段![]() 相等的两条线段;(不再另外添加辅助线)
相等的两条线段;(不再另外添加辅助线)
(2)探究:当点![]() 在什么位置时,四边形
在什么位置时,四边形![]() 是平行四边形?并判断四边形
是平行四边形?并判断四边形![]() 是什么特殊的平行四边形,请说明理由;
是什么特殊的平行四边形,请说明理由;
(3)在(2)的条件下,以点![]() 为圆心,
为圆心,![]() 为半径作圆,根据
为半径作圆,根据![]() 与平行四边形
与平行四边形![]() 四条边交点的总个数,求相应的
四条边交点的总个数,求相应的![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某快递公司计划购买A型和B型两种货车共8辆,其中每辆车的价格以及每辆车的运载量如下表:
A型 | B型 | |
价格(万元/台) | m | n |
运载量(吨/车) | 20 | 30 |
若购买A型货车1辆,B型货车3辆,共需67万元;若购买A型货车3辆,B型货车2辆,共需75万元.
(1)求m,n的值;
(2)若每辆A型货车每月运载量500吨,每辆B型货车每月运载量750吨,为确保这8辆车每月的运载量总和不少于4750吨,且该公司购买A型和B型货车的总费用不超过124万元.请你设计一个方案,使得购车总费用最少.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com