
����Ŀ���Ķ����ϣ�����֪������A��B�������Ϸֱ��ʾ������a��b��A��B����֮��ľ����ʾΪAB����������A��B����֮��ľ���AB=|a-b|������ʽ��|x3|�ļ��������������ϱ�ʾ������3�ĵ����ʾ������x�ĵ�֮��ľ��룮
�����������ϣ�����������⣺
![]()
��1����|x3|=4����x=______��
��2��ʽ��|x3|=|x+1|����x=______��
��3����|x3|+|x+1|=9������������x��ֵ��
���𰸡���1��7��-1����2��1����3��-3.5��5.5��
��������
��1�����ݾ���ֵ���ʣ���ɽ��.
��2��x �ǵ���3�뵽��-1�ľ�����ȣ�����-1��3֮��ģ����֪��x-3С��0��x+1����0����ɵõ����̣����x.
��3���������ۣ���ɵõ���.
�⣺��1��|x3|=4 �� x-3=4����x-3=-4 .
��ã�x=7����-1.
��2��|x3|=|x+1|
�ɾ���ֵ����,֪x-3![]() 0��x+1
0��x+1![]() 0.
0.
ԭʽΪ��3-x=x+1 ��ã�x=1
(3) |x3|+|x+1|=9
������3��-1֮��ľ���Ϊ4�����㷽�̵Ķ�Ӧ����-1����ߣ�������3���ұ�;
����-1����ߣ���x=-3.5.
����3���ұߣ���x=5.5
���ԣ�ԭ���̵Ľ�Ϊx=-3.5.����x=-3.5.
��x��ֵΪ-3.5��5.5



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���D��AB�ϣ���CD��CB����EΪBD���е㣬��FΪAC���е㣬����EF��CD�ڵ�M��
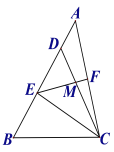
��1����֤��EF��![]() AC��
AC��
��2������AM������BAC��45����AM+DM=15��BE=9����CE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P������AB���Ϸ�������PAB=45�㣬PA=2����M������AB�ϵĶ���(��M�����A�غ�)���ֽ���P�Ƶ�A��˳ʱ�뷽����ת60������Q������M�Ƶ�P����ʱ�뷽����ת60������N������AQ��PM��PN����ֱ��QN.
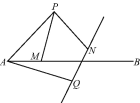
(1)��֤:AM=QN.
(2)ֱ��QN���Ե�PΪԲ������PN�ij�Ϊ�뾶��Բ�Ƿ�������е����?���������������ʱAM�ij���������������˵������.
(3)���Ե�PΪԲ������PN�ij�Ϊ�뾶��Բ������Qʱ��ֱ��д���ӻ�NQ�������뾶��Χ�ɵ����ε����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��6��0����B��8��5�������߶�OAƽ����CB����D��x��0����x���������ϣ������A�غϣ�������OC��AB��CD��BD��
��1����Խ���AC�ij���
��2����ODC����ABD������ֱ��ΪS1��S2����S��S1��S2����S����x�ĺ�������ʽ����̽���Ƿ���ڵ�DʹS����DBC�������ȣ�������ڣ������x��ֵ����ȡֵ��Χ������������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ���һԪ���η���x2��2x��1��0ʱ�����Dz��õ�һ�ַ�������ֱ������ϵ�л���������y��x2��ֱ��y��2x��1����ͼ��ĺ�������Ǹ÷��̵Ľ⣮
(1)���ٸ���һ������ͼ����x2��2x��1��0�Ľ�ķ�����
(2)��֪����y��x3��ͼ��(��ͼ)����x3��x��2��0�Ľ�(���������λ��Ч����)��
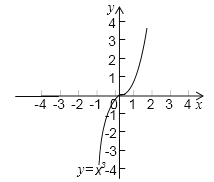
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����֪����y��ax2(a��0)��ͼ���ϵĵ�D��C��x���ϵĵ�A(��5��0)��B(3��0)����ABCD��DC��y��Ľ���ΪE(0��6)������a��ֵ��
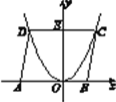
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() ��
��![]() Ϊ�����������������ϣ���
Ϊ�����������������ϣ���![]() ��ԭ��
��ԭ��![]() ����ߣ���
����ߣ���![]() ����
����![]() �ڵ�
�ڵ�![]() ���ұߣ���
���ұߣ���![]() ����
����![]() �ڵ�
�ڵ�![]() ����ߣ���
����ߣ���![]() ����
����![]() �ڵ�
�ڵ�![]() ���ұߣ���
���ұߣ���![]() �����������������ɣ���
�����������������ɣ���![]() ����ʾ�����ֱ�Ϊ �� ��
����ʾ�����ֱ�Ϊ �� ��
A.2018����2019B.1009����1010C.��2018��2019D.��1009��1009
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������Ӳֽ�������������ӣ�ÿ��������3�����β����2���������ε�����ɡ�Ӳֽ������ͼ���ַ�ʽ�ü����ü���߽��ϲ������ã�
A��������6�����棻 B��������4�������5�����档

����19��Ӳֽ�壬�ü�ʱ![]() ����A������������B������
����A������������B������
��1����![]() �Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
�Ĵ���ʽ�ֱ��ʾ�ü����IJ���͵���ĸ�����
��2�����ü����IJ���͵���ǡ��ȫ�����꣬���������ٸ����ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪A(0,a)��B(b, 0)����a��b���㣺 ![]() ����DΪx��������һ����
����DΪx��������һ����
(1)��A��B���������
(2)��ͼ����ADO��ƽ���߽�y���ڵ�C���� FΪ�߶�OD��һ���㣬����F��CD��ƽ���߽�y���ڵ�H���ҡ�AFH=45���� �ж��߶�AH��FD��AD���ߵ�������ϵ��������֤��

(3)��AOΪ����AΪ���Ƕ�����������ADO������DBA=30����ֱ��д����DAO�Ķ���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com