
【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M.
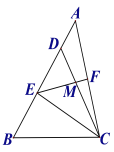
(1)求证:EF=![]() AC.
AC.
(2)连接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的长.
【答案】(1)见解析;(2)CE=12.
【解析】
(1)根据等腰三角形三线合一的性质可得CE⊥BD,再根据直角三角形斜边上的中线等于斜边的一半可得EF= ![]() AC;
AC;
(2)连接AM,证得△AEC是等腰直角三角形,EF垂直平分AC,AM=CM,则BC=AM+DM=15,在Rt△BEC中,利用勾股定理可得出CE的长。
(1)证明:
∵CD=CB,点E为BD的中点,
∴CE⊥BD,
∴∠AEC=90°,
∵在Rt△AEC中,点F为AC的中点,
∴EF=![]() AC;
AC;
(2)如图,连接AM,
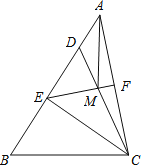
∵∠BAC=45°,CE⊥BD,
∴△AEC是等腰直角三角形,
∵点F为AC的中点,
∴EF垂直平分AC,
∴AM=CM,
∵CD=CM+DM=AM+DM,CD=CB,
∴BC=AM+DM=15,
∵BE=9,
在Rt△BEC中,
![]() .
.


 天天向上口算本系列答案
天天向上口算本系列答案科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料,回答以下问题:
我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.
例如![]() 是方程
是方程![]() 的一个解,对应点
的一个解,对应点![]() ,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点
,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点![]() 将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程
将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程![]() 的解.所以,我们就把条直线就叫做方程
的解.所以,我们就把条直线就叫做方程![]() 的图象.
的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.请问:
(1)已知![]() 、
、![]() 、
、![]() ,则点__________(填“A或
,则点__________(填“A或![]() 或
或![]() ”)在方程
”)在方程![]() 的图象上.
的图象上.
(2)求方程![]() 和方程
和方程![]() 图象的交点坐标.
图象的交点坐标.
(3)已知以关于![]() 的方程组
的方程组![]() 的解为坐标的点在方程
的解为坐标的点在方程![]() 的图象上,当
的图象上,当![]() 时,化简
时,化简![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=﹣2x+4的图象与x轴、y轴分别交于点A、B,点C是OA的中点,过点C作CD⊥OA于C交一次函数图象于点D,P是OB上一动点,则PC+PD的最小值为( )

A.4B.![]() C.2
C.2![]() D.2
D.2![]() +2
+2
查看答案和解析>>
科目:初中数学 来源: 题型:
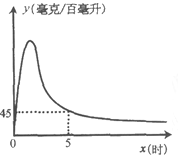
【题目】实验数据显示,一般成人喝半斤低度白酒后,1.5时内其血液中酒精含量y(毫克/百毫升)与时间![]() (时)的关系可近似地用二次函数
(时)的关系可近似地用二次函数![]() 刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数
刻画;1.5时后(包括1.5时)y与x可近似地用反比例函数![]() (k>0)刻画(如图所示).
(k>0)刻画(如图所示).
(1)根据上述数学模型计算:
①喝酒后几时血液中的酒精含量达到最大值?最大值为多少?
②当![]() =5时,y=45.求k的值.
=5时,y=45.求k的值.
(2)按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路.参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,第二天早上7:00能否驾车去上班?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
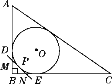
A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
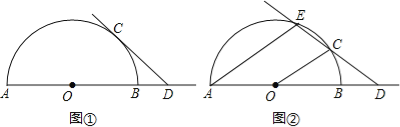
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道:点A.B在数轴上分别表示有理数a、b,A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|a-b|.所以式子|x3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,解答下列问题:
![]()
(1)若|x3|=4,则x=______;
(2)式子|x3|=|x+1|,则x=______;
(3)若|x3|+|x+1|=9,借助数轴求x的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com