
【题目】已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
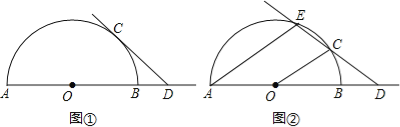
【答案】(1) ∠ODC=45°;(2) AE=OD.理由见解析;∠ODC=36°.
【解析】试题分析:(1)连接OC,因为CD是⊙O的切线,得出∠OCD=90°,由OC=CD,得出∠ODC=∠COD,即可求得.
(2)连接OE,
①证明△AOE≌△OCD,即可得AE=OD;
②利用等腰三角形及平行线的性质,可求得∠ODC的度数.
试题解析:(1)如图①,连接OC,
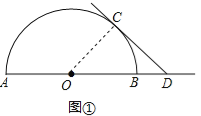
∵OC=OA,CD=OA,
∴OC=CD,
∴∠ODC=∠COD,
∵CD是⊙O的切线,
∴∠OCD=90°,
∴∠ODC=45°;
(2)如图②,连接OE.
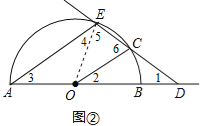
∵CD=OA,∴CD=OC=OE=OA,
∴∠1=∠2,∠3=∠4.
∵AE∥OC,
∴∠2=∠3.
设∠ODC=∠1=x,则∠2=∠3=∠4=x.
∴∠AOE=∠OCD=180°-2x.
①AE=OD.理由如下:
在△AOE与△OCD中,
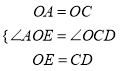
∴△AOE≌△OCD(SAS),
∴AE=OD.
②∠6=∠1+∠2=2x.
∵OE=OC,∴∠5=∠6=2x.
∵AE∥OC,
∴∠4+∠5+∠6=180°,即:x+2x+2x=180°,
∴x=36°.
∴∠ODC=36°.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线p: ![]() 的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是
的顶点为C,与x轴相交于A、B两点(点A在点B左侧),点C关于x轴的对称点为C′,我们称以A为顶点且过点C′,对称轴与y轴平行的抛物线为抛物线p的“梦之星”抛物线,直线AC′为抛物线p的“梦之星”直线.若一条抛物线的“梦之星”抛物线和“梦之星”直线分别是![]() 和y=2x+2,则这条抛物线的解析式为____________________.
和y=2x+2,则这条抛物线的解析式为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在AB上,且CD=CB,点E为BD的中点,点F为AC的中点,连结EF交CD于点M.
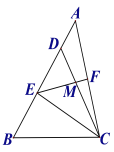
(1)求证:EF=![]() AC.
AC.
(2)连接AM,若∠BAC=45°,AM+DM=15,BE=9,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
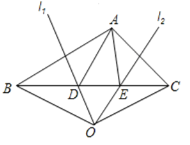
【题目】如图,在△ABC中,AB边的垂直平分线l1交BC于点D,AC边的垂直平分线l2交BC于点E,l1与l2相交于点O,连结0B,OC.若△ADE的周长为12cm,△OBC的周长为32cm.
(1)求线段BC的长;
(2)连结OA,求线段OA的长;
(3)若∠BAC=n°(n>90),直接写出∠DAE的度数 °.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:根据《中国铁路中长期发展规划》,预计到2020年底,我国建设城际轨道交通的公里数是客运专线的2倍。其中建设城际轨道交通约投入8000亿元,客运专线约投入3500亿元。据了解,建设每公里城际轨道交通与客运专线共需1.5亿元。预计到2020年底,我国将建设城际轨道交通和客运专线分别约多少公里?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,以点C为圆心,BC为半径的圆交AB于点D,交AC于点E.
(1)若∠A=25°,求![]() 的度数;
的度数;
(2)若BC=9,AC=12,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°到点Q,将点M绕点P按逆时针方向旋转60°到点N,连接AQ,PM,PN,作直线QN.
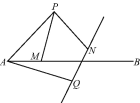
(1)求证:AM=QN.
(2)直线QN与以点P为圆心,以PN的长为半径的圆是否存在相切的情况?若存在,请求出此时AM的长,若不存在,请说明理由.
(3)当以点P为圆心,以PN的长为半径的圆经过点Q时,直接写出劣弧NQ与两条半径所围成的扇形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A(6,0),B(8,5),将线段OA平移至CB,点D(x,0)在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)求对角线AC的长;
(2)△ODC与△ABD的面积分别记为S1,S2,设S=S1﹣S2,求S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等,如果存在,请求出x的值(或取值范围);如果不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用正方形硬纸板做三棱柱盒子,每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪(裁剪后边角料不再利用)
A方法:剪6个侧面; B方法:剪4个侧面和5个底面。

现有19张硬纸板,裁剪时![]() 张用A方法,其余用B方法。
张用A方法,其余用B方法。
(1)用![]() 的代数式分别表示裁剪出的侧面和底面的个数;
的代数式分别表示裁剪出的侧面和底面的个数;
(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com