
【题目】如图,点P在射线AB的上方,且∠PAB=45°,PA=2,点M是射线AB上的动点(点M不与点A重合),现将点P绕点A按顺时针方向旋转60°到点Q,将点M绕点P按逆时针方向旋转60°到点N,连接AQ,PM,PN,作直线QN.
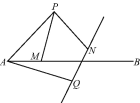
(1)求证:AM=QN.
(2)直线QN与以点P为圆心,以PN的长为半径的圆是否存在相切的情况?若存在,请求出此时AM的长,若不存在,请说明理由.
(3)当以点P为圆心,以PN的长为半径的圆经过点Q时,直接写出劣弧NQ与两条半径所围成的扇形的面积.
【答案】(1)证明见解析; (2)存在.理由见解析; (3)劣弧NQ与两条半径所围成的扇形的面积为π.
【解析】
(1)根据旋转的旋转判断出△APQ为等边三角形,再判断出∠APM=∠QPN,从而得出△APM≌△QPN即可;
(2)由直线和圆相切得出∠AMP=∠QNP=90°,再用勾股定理即可求出结论;
(3)先判断出PA=PQ,再判断出PQ=PN=PM,进而求出∠QPM=30°,即可求出∠QPN=90°,最后用扇形的面积公式即可.
(1)如图1,连接PQ,由点P绕点A按顺时针方向旋转60°到点Q,
可得AP=AQ,∠PAQ=60°,
∴△APQ为等边三角形,
∴PA=PQ,∠APQ=60°,
由点M绕点P按逆时针方向旋转60°到点N,
可得PM=PN,∠MPN=60°,
∴∠APM=∠QPN,则△APM≌△QPN(SAS),
∴AM=QN.
(2)存在.理由如下:
如图2,由(1)中的证明可知△APM≌△QPN,
∴∠AMP=∠QNP,
∵直线QN与以点P为圆心,以PN的长为半径的圆相切,
∴∠AMP=∠QNP=90°,即PN⊥QN.
在Rt△APM中,∠PAB=45°,PA=2,
∴AM=![]() .
.
(3)由(1)知△APQ是等边三角形,
∴PA=PQ,∠APQ=60°.
∵以点P为圆心,以PN的长为半径的圆经过点Q,
∴PN=PQ=PA.
∵PM=PN,
∴PA=PM,
∵∠PAB=45°,
∴∠APM=90°,
∴∠MPQ=∠APM-∠APQ=30°.
∵∠MPN=60°,
∴∠QPN=90°,
∴劣弧NQ与两条半径所围成的扇形的面积是扇形QPN的面积,而此扇形的圆心角∠QPN=90°,半径为PN=PM=PA=2.
∴劣弧NQ与两条半径所围成的扇形的面积=![]() =π.
=π.


科目:初中数学 来源: 题型:
【题目】如图,在一条笔直的东西向海岸线l上有一长为1.5km的码头MN和灯塔C,灯塔C距码头的东端N有20km.一轮船以36km/h的速度航行,上午10:00在A处测得灯塔C位于轮船的北偏西30°方向,上午10:40在B处测得灯塔C位于轮船的北偏东60°方向,且与灯塔C相距12km.
(1)若轮船照此速度与航向航向,何时到达海岸线?
(2)若轮船不改变航向,该轮船能否停靠在码头?请说明理由(参考数据: ![]() ≈1.4,
≈1.4, ![]() ≈1.7).
≈1.7).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB,BC分别相切于点D,E,过劣弧DE(不包括端点D,E)上任一点P作⊙O的切线MN,与AB,BC分别交于点M,N,若⊙O的半径为r,则Rt△MBN的周长为( )
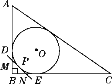
A. r B. ![]() r C. 2r D.
r C. 2r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
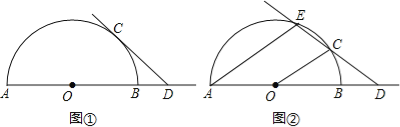
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下述材料:
下述形式的繁分数叫做有限连分数,其中n是自然数,a0是整数,a1,a2,a3,…,an是正整数:

其中![]() 称为部分商。
称为部分商。
按照以下方式可将任何一个分数转化为连分数的形式:![]() ,则
,则![]() ;考虑
;考虑![]() 的倒数,有
的倒数,有![]() ,从而
,从而 ;再考虑
;再考虑![]() 的倒数,有
的倒数,有![]() ,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;
,于是得到a的连分数展开式,它有4个部分商:3,1,3,3;

可利用连分数来求二元一次不定方程的特殊解,以![]() 为例,首先将
为例,首先将![]() 写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数
写成连分数的形式,如上所示;其次,数部分商的个数,本例是偶数个部分商(奇数情况请见下例);最后计算倒数第二个渐近分数 ,从而
,从而![]() 是一个特解。
是一个特解。
考虑不定方程![]() ,先将
,先将![]() 写成连分数的形式:
写成连分数的形式: 。
。
注意到此连分数有奇数个部分商,将之改写为偶数个部分商的形式:

计算倒数第二个渐近分数: ,所以
,所以![]() 是
是![]() 的一个特解。
的一个特解。
对于分式,有类似的连分式的概念,利用将分数展开为连分数的方法,可以将分式展开为连分式。例如![]() 的连分式展开式如下,它有3个部分商:
的连分式展开式如下,它有3个部分商:![]()
![]() ;
;

再例如, ,它有4个部分商:1,
,它有4个部分商:1,![]() 。
。
请阅读上述材料,利用所讲述的方法,解决下述两个问题
(1)找出两个关于x的多项式p和q,使得![]() 。
。
(2)找出两个关于x的多项式u和v,使得![]() 。
。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
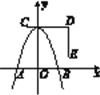
【题目】如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C-D-E上移动,若点C,D,E的坐标分别为(-1,4),(3,4),(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道:点A.B在数轴上分别表示有理数a、b,A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|a-b|.所以式子|x3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,解答下列问题:
![]()
(1)若|x3|=4,则x=______;
(2)式子|x3|=|x+1|,则x=______;
(3)若|x3|+|x+1|=9,借助数轴求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线l1∥l2,线段AB在直线l1上,BC垂直于l1交l2于点C,且AB=BC,P是线段BC上异于两端点的一点,过点P的直线分别交l2、l1于点D. E(点A. E位于点B的两侧),满足BP=BE,连接AP、CE.
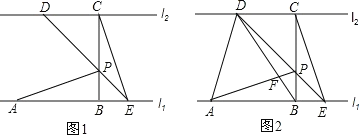
(1)求证:△ABP≌△CBE;
(2)连结AD、BD,BD与AP相交于点F. 如图2.
①当![]() =2时,求证:AP⊥BD;
=2时,求证:AP⊥BD;
②当![]() =n(n>1)时,设△DAP的面积为S1,△EPC的面积为S2,求
=n(n>1)时,设△DAP的面积为S1,△EPC的面积为S2,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com