【题目】列方程解应用题：根据《中国铁路中长期发展规划》，预计到2020年底，我国建设城际轨道交通的公里数是客运专线的2倍。其中建设城际轨道交通约投入8000亿元，客运专线约投入3500亿元。据了解，建设每公里城际轨道交通与客运专线共需1.5亿元。预计到2020年底，我国将建设城际轨道交通和客运专线分别约多少公里？
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，在△ABC中，边AB、AC的垂直平分线分别交BC于D、E．
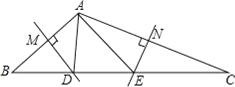
（1）若BC=10，求△ADE的周长；
（2） 设直线DM、EN交于点O
①试判断点O是否在BC的垂直平分线上，并说明理由；
②若∠BAC=100°，求∠BOC的度数
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，一次函数y＝﹣2x+4的图象与x轴、y轴分别交于点A、B，点C是OA的中点，过点C作CD⊥OA于C交一次函数图象于点D，P是OB上一动点，则PC+PD的最小值为（ ）
A.4B.
C.2
D.2+2
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，Rt△ABC的内切圆⊙O与两直角边AB，BC分别相切于点D，E，过劣弧DE(不包括端点D，E)上任一点P作⊙O的切线MN，与AB，BC分别交于点M，N，若⊙O的半径为r，则Rt△MBN的周长为( )
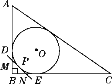
A. r B. 
r C. 2r D. 
r
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图是考古学家发现的古代钱币的一部分，合肥一中的小明正好学习了圆的知识，他想求其外圆半径，连接外圆上的两点A，B，并使AB与内圆相切于点D，作CD⊥AB交外圆于点C.测得CD=10 cm，AB=60 cm，则这个钱币的外圆半径为__cm.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知AB是半圆O的直径，点C是半圆O上的动点，点D是线段AB延长线上的动点，在运动过程中，保持CD=OA．
（1）当直线CD与半圆O相切时（如图①），求∠ODC的度数；
（2）当直线CD与半圆O相交时（如图②），设另一交点为E，连接AE，若AE∥OC，
①AE与OD的大小有什么关系？为什么？
②求∠ODC的度数．
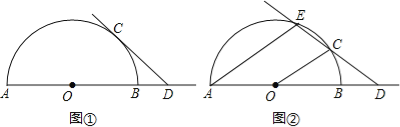
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】请阅读下述材料：
下述形式的繁分数叫做有限连分数，其中n是自然数，a0是整数，a1，a2，a3，…，an是正整数：
其中
称为部分商。
按照以下方式可将任何一个分数转化为连分数的形式：
，则
；考虑
的倒数，有
，从而
；再考虑
的倒数，有
，于是得到a的连分数展开式，它有4个部分商：3，1，3，3；
可利用连分数来求二元一次不定方程的特殊解，以
为例，首先将
写成连分数的形式，如上所示；其次，数部分商的个数，本例是偶数个部分商（奇数情况请见下例）；最后计算倒数第二个渐近分数
，从而
是一个特解。
考虑不定方程
，先将
写成连分数的形式：
。
注意到此连分数有奇数个部分商，将之改写为偶数个部分商的形式：
计算倒数第二个渐近分数：
，所以
是的一个特解。
对于分式，有类似的连分式的概念，利用将分数展开为连分数的方法，可以将分式展开为连分式。例如
的连分式展开式如下，它有3个部分商：
；
再例如，
，它有4个部分商：1，
。
请阅读上述材料，利用所讲述的方法，解决下述两个问题
（1）找出两个关于x的多项式p和q，使得
。
（2）找出两个关于x的多项式u和v，使得
。
查看答案和解析>>
科目：初中数学 来源： 题型：
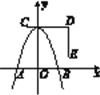
【题目】如图，一条抛物线与x轴相交于A，B两点，其顶点P在折线C－D－E上移动，若点C，D，E的坐标分别为(－1，4)，(3，4)，(3，1)，点B的横坐标的最小值为1，则点A的横坐标的最大值为________．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】图中的五个半圆，邻近的两半圆相切，两只小虫同时出发，以相同的速度从A点到B点，甲虫沿ADA1、A1EA2、A2FA3、A3GB路线爬行，乙虫沿ACB路线爬行，则下列结论正确的是（ ）
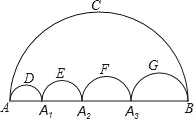
A. 甲先到B点 B. 乙先到B点 C. 甲、乙同时到B D. 无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
