
【题目】如图,已知点A(6,0),B(8,5),将线段OA平移至CB,点D(x,0)在x轴正半轴上(不与点A重合),连接OC,AB,CD,BD.
(1)求对角线AC的长;
(2)△ODC与△ABD的面积分别记为S1,S2,设S=S1﹣S2,求S关于x的函数解析式,并探究是否存在点D使S与△DBC的面积相等,如果存在,请求出x的值(或取值范围);如果不存在,请说明理由.

【答案】(1)![]() ;(2)D(x,0)(x>6)
;(2)D(x,0)(x>6)
【解析】
(1)根据平移的性质可以求得点C的坐标,然后根据两点间的距离公式即可求得AC的长;
(2)根据题意,可以分别表示出S1,S2,从而可以得到S关于x的函数解析式,由图和题目中的条件可以求得△CDB的面积,从而可以求得满足条件的点D的坐标,本题得以解决.
(1)由题意知,将线段OA平移至CB,
∴四边形OABC为平行四边形.
又∵A(6,0),B(8,5),∴点C(2,5).
过点C作CE⊥OA于E,连接AC,在Rt△CEA中,

AC=![]() =
=![]() =
=![]() .
.
(2)∵点D的坐标为(x,0),
若点D在线段OA上,即当0<x<6时,
![]() ,
,![]() ,
,
∴![]() =5x-15.
=5x-15.
若点D在OA的延长线上,即当x>6时,
![]() ,
,![]() ,
,
∴![]() =15.
=15.
由上可得,![]()
∵![]() ,
,
当0<x<6时,![]() 时,x=6(与A重合,不合题意,舍去);
时,x=6(与A重合,不合题意,舍去);
当x>6时,![]() ,点D在OA延长线上的任意一点处都可满足条件,
,点D在OA延长线上的任意一点处都可满足条件,
∴点D所在位置为D(x,0)(x>6).


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:初中数学 来源: 题型:
【题目】阅读材料,回答以下问题:
我们知道,二元一次方程有无数个解,在平面直角坐标系中,我们标出以这个方程的解为坐标的点,就会发现这些点在同一条直线上.
例如![]() 是方程
是方程![]() 的一个解,对应点
的一个解,对应点![]() ,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点
,如下图所示,我们在平面直角坐标系中将其标出,另外方程的解还有对应点![]() 将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程
将这些点连起来正是一条直线,反过来,在这条直线上任取一点,这个点的坐标也是方程![]() 的解.所以,我们就把条直线就叫做方程
的解.所以,我们就把条直线就叫做方程![]() 的图象.
的图象.
一般的,任意二元一次方程解的对应点连成的直线就叫这个方程的图象.请问:
(1)已知![]() 、
、![]() 、
、![]() ,则点__________(填“A或
,则点__________(填“A或![]() 或
或![]() ”)在方程
”)在方程![]() 的图象上.
的图象上.
(2)求方程![]() 和方程
和方程![]() 图象的交点坐标.
图象的交点坐标.
(3)已知以关于![]() 的方程组
的方程组![]() 的解为坐标的点在方程
的解为坐标的点在方程![]() 的图象上,当
的图象上,当![]() 时,化简
时,化简![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB是半圆O的直径,点C是半圆O上的动点,点D是线段AB延长线上的动点,在运动过程中,保持CD=OA.
(1)当直线CD与半圆O相切时(如图①),求∠ODC的度数;
(2)当直线CD与半圆O相交时(如图②),设另一交点为E,连接AE,若AE∥OC,
①AE与OD的大小有什么关系?为什么?
②求∠ODC的度数.
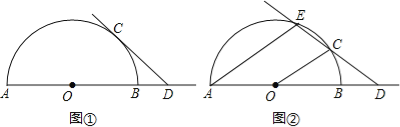
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=3,点E,F分别在CD,AD上,CE=DF,BE,CF相交于点G.若图中阴影部分的面积与正方形ABCD的面积之比为2:3,则△BCG的周长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
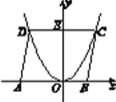
【题目】如图,一条抛物线与x轴相交于A,B两点,其顶点P在折线C-D-E上移动,若点C,D,E的坐标分别为(-1,4),(3,4),(3,1),点B的横坐标的最小值为1,则点A的横坐标的最大值为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
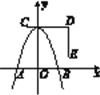
【题目】如图所示,已知函数y=ax2(a≠0)的图象上的点D,C与x轴上的点A(-5,0)和B(3,0)构成ABCD,DC与y轴的交点为E(0,6),试求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:我们知道:点A.B在数轴上分别表示有理数a、b,A.B两点之间的距离表示为AB,在数轴上A.B两点之间的距离AB=|a-b|.所以式子|x3|的几何意义是数轴上表示有理数3的点与表示有理数x的点之间的距离.
根据上述材料,解答下列问题:
![]()
(1)若|x3|=4,则x=______;
(2)式子|x3|=|x+1|,则x=______;
(3)若|x3|+|x+1|=9,借助数轴求x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市政府于2017年初投资了112万元,建成40个公共自行车站点、配置720辆公共自行车正式启用公共自行车租贷系统:今后将逐年增加投资,用于建设新站点、配置公共自行车.预计2019年将投资340.5万元,新建120个公共自行车站点、配置2205辆公共自行车.
(1)每个站点的造价和公共自行车的单价分别是多少万元?
(2)若2017年到2019年市政府配置公共自行车数量的年平均增长率相同,请你求出2018年市政府配置公共自行车的数量.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com