
【题目】股民王先生上周星期五买进某公司股票1000股,每股18元,本周该股票的涨跌情况如表(正数表示价格比前一天上涨,负数表示价格比前一天下跌,单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
(1)星期三结束时,该股票每股多少元?
(2)该股票本周内每股的最高价和最低价分别是多少元?
科目:初中数学 来源: 题型:
【题目】春节前,安徽黄山脚下的小村庄的集市上,人山人海,还有人在摆“摸彩”游戏,只见他手拿一个黑色的袋子,内装大小、形状、质量完全相同的白球20只,且每一个球上都写有号码(1~20号)和1只红球,规定:每次只摸一只球.摸前交1元钱且在1~20内写一个号码,摸到红球奖5元,摸到号码数与你写的号码相同奖10元.
(1)你认为该游戏对“摸彩”者有利吗?说明你的理由.
(2)若一个“摸彩”者多次摸奖后,他平均每次将获利或损失多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
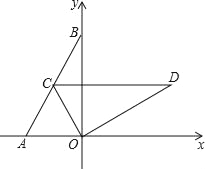
【题目】已知如图,在直角坐标系xOy中,点A,点B坐标分别为(﹣1,0),(0,![]() ),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
),连结AB,OD由△AOB绕O点顺时针旋转60°而得.
(1)求点C的坐标;
(2)△AOB绕点O顺时针旋转60°所扫过的面积;
(3)线段AB绕点O顺时针旋转60°所扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两条直线AB、CD相交于点O,且∠AOC=90°,射线OM从OB开始绕O点逆时针方向旋转,速度为15°/s,射线ON同时从OD开始绕O点顺时针方向旋转,速度为12°/s.两条射线OM、ON同时运动,运动时间为t秒.(本题出现的角均小于平角)
(1)当t=2时,∠MON的度数为 ,∠BON的度数为 ;∠MOC的度数为
(2)当0<t<12时,若∠AOM=3∠AON-60°,试求出t的值;
(3)当0<t<6时,探究![]() 的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?
的值,问:t满足怎样的条件是定值;满足怎样的条件不是定值?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象经过点A(﹣1,0)、点B(3,0)、点C(4,y1),若点D(x2,y2)是抛物线上任意一点,有下列结论:
①二次函数y=ax2+bx+c的最小值为﹣4a;
②若﹣1≤x2≤4,则0≤y2≤5a;
③若y2>y1,则x2>4;
④一元二次方程cx2+bx+a=0的两个根为﹣1和![]()
其中正确结论的个数是( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点A,点(﹣2,m)和(﹣5,n)在该抛物线上,则下列结论中不正确的是( )
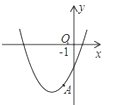
A. b2>4ac B. m>n C. 方程ax2+bx+c=﹣4的两根为﹣5或﹣1 D. ax2+bx+c≥﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
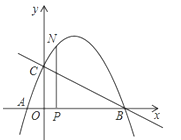
【题目】如图,抛物线与x轴交于点A(﹣![]() , 0),点B(2,0),与y轴交于点C(0,1),连接BC.
, 0),点B(2,0),与y轴交于点C(0,1),连接BC.
(1)求抛物线的解析式;
(2)N为抛物线上的一个动点,过点N作NP⊥x轴于点P,设点N的横坐标为t(﹣![]() <t<2),求△ABN的面积s与t的函数解析式;
<t<2),求△ABN的面积s与t的函数解析式;
(3)若0<t<2且t≠0时,△OPN∽△COB,求点N的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:
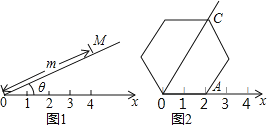
如图1,在平面内选一定点O,引一条有方向的射线Ox,再选定一个单位长度,那么平面上任一点M的位置可由∠MOx的度数θ与OM的长度m确定,有序数对(θ,m)称为M点的“极坐标”,这样建立的坐标系称为“极坐标系”.
应用:在图2的极坐标系下,如果正六边形的边长为2,有一边OA在射线Ox上,则正六边形的顶点C的极坐标应记为( )
A.(60°,4) B.(45°,4) C.(60°,2![]() ) D.(50°,2
) D.(50°,2![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com