
【题目】如图,已知顶点为(﹣3,﹣6)的抛物线y=ax2+bx+c经过点A,点(﹣2,m)和(﹣5,n)在该抛物线上,则下列结论中不正确的是( )
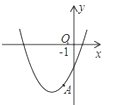
A. b2>4ac B. m>n C. 方程ax2+bx+c=﹣4的两根为﹣5或﹣1 D. ax2+bx+c≥﹣6
【答案】B
【解析】
由抛物线与x轴有两个交点则可对A进行判断;根据抛物线上的点离对称轴的远近,则可对B进行判断;根据二次函数的对称性可对C进行判断;由于抛物线开口向上,有最小值则可对D进行判断.
A、图象与x轴有两个交点,方程ax2+bx+c=0有两个不相等的实数根,b2-4ac>0所以b2>4ac,故A选项正确;
B、抛物线的对称轴为直线x=-3,因为-5离对称轴的距离大于-2离对称轴的距离,所以m<n,故B选项错误;
C、根据抛物线的对称性可知,(-1,n)关于对称轴的对称点为(-5,n),所以关于x的一元二次方程ax2+bx+c=-n的两根为-5和-1,故C选项正确;
D、抛物线的开口向上,函数有最小值,因为抛物线的最小值为-6,所以ax2+bx+c≥-6,故D选项正确,
故选B.


科目:初中数学 来源: 题型:
【题目】根据下列问题,列出关于x的方程,并将其化成ax2+bx+c=0(a≠0)的形式:
(1)一个长方形的宽比长少3,面积是75,求长方形的长x;
(2)两个连续偶数的积为168,求较小的偶数x;
(3)一个直角三角形的两条直角边的长的和是20,面积是25,求其中一条直角边的长x.
查看答案和解析>>
科目:初中数学 来源: 题型:
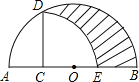
【题目】如图,AB为半圆O的直径,C为AO的中点,CD⊥AB交半圆于点D,以C为圆心,CD为半径画弧交AB于E点,若AB=4,则图中阴影部分的面积是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】股民王先生上周星期五买进某公司股票1000股,每股18元,本周该股票的涨跌情况如表(正数表示价格比前一天上涨,负数表示价格比前一天下跌,单位:元)
星期 | 一 | 二 | 三 | 四 | 五 |
每股涨跌 |
|
|
|
|
|
(1)星期三结束时,该股票每股多少元?
(2)该股票本周内每股的最高价和最低价分别是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx﹣3.
(1)若函数图象经过点(1,﹣4),(﹣1,0),求a,b的值;
(2)证明:若2a﹣b=1,则存在一条确定的直线始终与该函数图象交于两点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,我们把横、纵坐标都是整数的点叫做整点.如图,已知⊙O的半径为5,则抛物线![]() 与该圆所围成的阴影部分(不包括边界)的整点个数是( )
与该圆所围成的阴影部分(不包括边界)的整点个数是( )

A. 24 B. 23 C. 22 D. 21
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某自行车厂一周计划生产1400辆自行车,平均每天生产200辆,由于各种原因实际每天生产量与计划量相比有出入.下表是某周的生产情况(超产为正、减产为负):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 |
|
|
|
|
|
|
|
(1)根据记录可知前三天共生产______辆.
(2)产量最多的一天比产量最少的一天多生产_______辆.
(3)该厂实行每周计件工资制,每生产一辆车可得60元,若超额完成任务,则超过部分每辆另奖15元;少生产一辆扣15元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为解决农村燃气困难,在P处建立了一个燃气站,从P站分别向A、B、C村铺设燃气管道。已知B村在A村的北偏东60°方向,距离A村2.4km,C村在A村的正东方向,距离A村1.8km,要使此工程费用最省,管道PA+PB+PC之和需最短,则最短长度为______________km.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BE、CF分别是钝角△ABC(∠A>90°)的高,在BE上截取BP=AC,在CF的延长线截取CQ=AB,连结AP、AQ,请推测AP与AQ的数量和位置关系并加以证明。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com