
【题目】根据题意,解答问题:
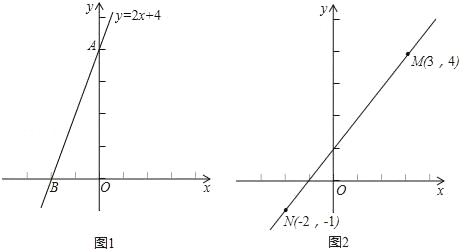
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)点D的坐标为(2,0).
;(3)点D的坐标为(2,0).
【解析】分析:(1)由一次函数解析式求得点A、B的坐标,则易求直角△AOB的两直角边OB、OA的长度,所以在该直角三角形中利用勾股定理即可求线段AB的长度;
(2)如图2,过M点作x轴的垂线MF,过N作y轴的垂线NE,MF和NE交于点C,构造直角△MNC,则在该直角三角形中利用勾股定理来求求点M与点N间的距离;
(3)如图3,设点D坐标为(m,0),连结ND,MD,过N作NG垂直x轴于G,过M作MH垂直x轴于H.在直角△DGN和直角△MDH中,利用勾股定理得到关于m的方程12+(m+2)=42+(3-m)2
通过解方程即可求得m的值,则易求点D的坐标.
详解:(1)令x=0,得y=4,即A(0,4).
令y=0,得x=-2,即B(-2,0).
在Rt△AOB中,根据勾股定理有:
AB=![]() ;
;
(2)如图2,过M点作x轴的垂线MF,过N作y轴的垂线NE,MF和NE交于点C.
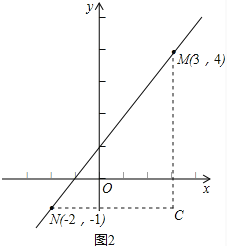
根据题意:MC=4-(-1)=5,NC=3-(-2)=5.
则在Rt△MCN中,根据勾股定理有:
MN=![]() ;
;
(3)如图3,设点D坐标为(m,0),连结ND,MD,
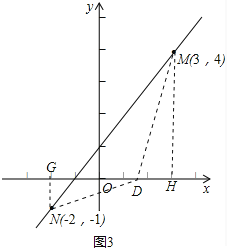
过N作NG垂直x轴于G,过M作MH垂直x轴于H.
则GD=|m-(-2)|,GN=1,DN2=GN2+GD2=12+(m+2)2
MH=4,DH=|3-m|,DM2=MH2+DH2=42+(3-m)2
∵DM=DN,
∴DM2=DN2
即12+(m+2)=42+(3-m)2
整理得:10m=20得m=2
∴点D的坐标为(2,0).


科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是矩形,∠EDC=∠CAB,∠DEC=90°.

(1)求证:AC∥DE;
(2)过点B作BF⊥AC于点F,连接EF,试判别四边形BCEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列单项式:![]() ,
,![]() ,
,![]() ,
,![]() ,…
,…![]() ,
,![]() ,…写出第
,…写出第![]() 个单项式,为了解这个问题,特提供下面的解题思路.
个单项式,为了解这个问题,特提供下面的解题思路.
![]() 这组单项式的系数的符号,绝对值规律是什么?
这组单项式的系数的符号,绝对值规律是什么?
![]() 这组单项式的次数的规律是什么?
这组单项式的次数的规律是什么?
![]() 根据上面的归纳,你可以猜想出第
根据上面的归纳,你可以猜想出第![]() 个单项式是什么?
个单项式是什么?
![]() 请你根据猜想,请写出第
请你根据猜想,请写出第![]() 个,第
个,第![]() 个单项式.
个单项式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: ![]() 对称.
对称. 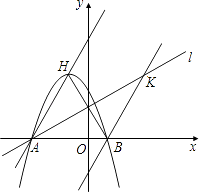
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式; 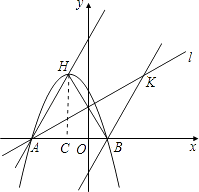
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值. 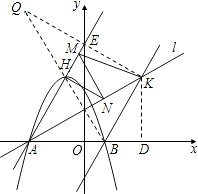
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)某自行车厂一周计划生产700辆自行车,平均每天生产自行车100辆,由于各种原因,实际每天生产量与计划每天生产量相比有出入。下表是某周的自行车生产情况(超计划生产量为正、不足计划生产量为负,单位:辆):
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
增减 | +8 | -2 | -3 | +16 | -9 | +10 | -11 |
(1)根据记录可知前三天共生产自行车 辆;
(2)产量最多的一天比产量最少的一天生产 辆;
(3)若该厂实行按生产的自行车数量的多少计工资,即计件工资制。如果每生产一辆自行车就可以得人民币60 元,超额完多成任务,每超一辆可多得 15 元;若不足计划数的,每少生产一辆扣 15 元,那么该厂工人这一周的工资总额是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
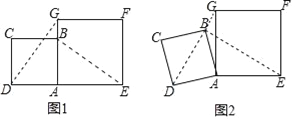
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
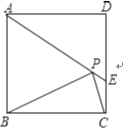
【题目】如图,在正方形ABCD中,AD=![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
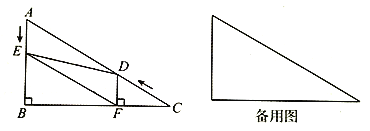
【题目】如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)当四边形BFDE是矩形时,求t的值;
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.×
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com