
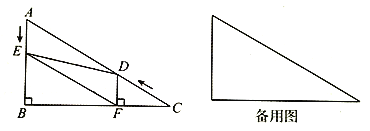
【题目】如图,在Rt△ABC中,∠B=90°,∠C=30°,AC=48,点D从点C出发沿CA方向以每秒4个单位长的速度向点A匀速运动,同时点E从点A出发沿AB方向以每秒2个单位长的速度向点B匀速运动,当其中一个点到达终点,另一个点也随之停止运动,设点D、E运动的时间是t秒(t>0),过点D作DF⊥BC于点F,连接DE、EF.
(1)求证:AE=DF;
(2)当四边形BFDE是矩形时,求t的值;
(3)四边形AEFD能够成为菱形吗?如果能,求出相应的t值;如果不能,说明理由.×
【答案】(1)证明见解析;(2)6s;(2)8s.
【解析】分析:(1)由∠DFC=90°,∠C=30°,证出DF=2t=AE;
(2)当四边形BEDF是矩形时,△DEF为直角三角形且∠EDF=90°,求出t的值即可;
(3)先证明四边形AEFD为平行四边形.得出AB=3,AD=AC-DC=48-4t,若△DEF为等边三角形,则四边形AEFD为菱形,得出AE=AD,2t=48-4t,求出t的值即可;
详解:(1)在Rt△CDF中,∠C=30°,
∴DF=![]() CD,
CD,
∴DF=![]() 4t=2t,
4t=2t,
又∵AE=2t,
∴AE=DF.
(2)当四边形BFDE是矩形时,有BE=DF,
∵Rt△ABC中,∠C=30°
∴AB=![]() AC=
AC=![]() ×48=24,
×48=24,
∴BE=AB-AE=24-2t,
∴24-2t=2t,
∴t=6.
(3)∵∠B=90°,DF⊥BC
∴AE∥DF,∵AE=DF,
∴四边形AEFD是平行四边形,
由(1)知:四边形AEFD是平行四边形
则当AE=AD时,四边形AEFD是菱形
∴2t=48-4t,
解得t=8,又∵t≤![]() =
=![]() =12,
=12,
∴t=8适合题意,
故当t=8s时,四边形AEFD是菱形.


科目:初中数学 来源: 题型:
【题目】根据题意,解答问题:
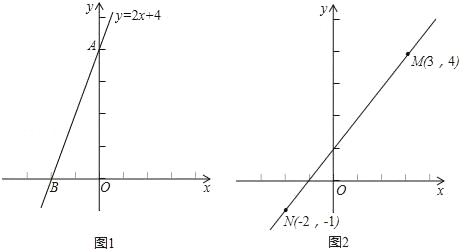
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人用![]() 元购买了
元购买了![]() 套儿童服装,准备以一定价格出售,如果以每套儿童服装
套儿童服装,准备以一定价格出售,如果以每套儿童服装![]() 元的价格为标准,超出的记作正数,不足的记作负数,记录如下:
元的价格为标准,超出的记作正数,不足的记作负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元)
(单位:元)
请你帮他计算出当他卖完这八套儿童服装后,赚了还是赔了,赚(或赔)了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为3cm,动点P从B点出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达A点停止运动;另一动点Q同时从B点出发,以1cm/s的速度沿着边BA向A点运动,到达A点停止运动.设P点运动时间为x(s),△BPQ的面积为y(cm2),则y关于x的函数图象是( )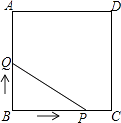
A.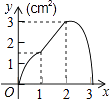
B.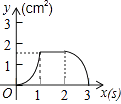
C.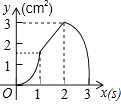
D.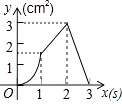
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场购进一种每件价格为100元的新商品,在商场试销发现:销售单价x(元/件)与每天销售量y(件)之间满足如图所示的关系: 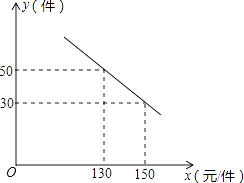
(1)求出y与x之间的函数关系式;
(2)写出每天的利润W与销售单价x之间的函数关系式;若你是商场负责人,会将售价定为多少,来保证每天获得的利润最大,最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com