
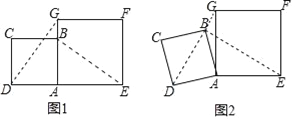
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
【答案】(1)见解析 (2)![]() +
+![]()
【解析】分析:(1)延长EB交DG于点H,先证出Rt△ADG≌Rt△ABE,得出∠AGD=∠AEB,再根据∠HBG=∠EBA,得出∠HGB+∠HBG=90°即可;
(2)过点A作AP⊥BD交BD于点P,根据△DAG≌△BAE得出DG=BE,根据AD=2∠PDA=45°,∠APD=90°,求出AP、DP,利用勾股定理求出PG,再根据DG=DP+PG求出DG,最后根据DG=BE即可得出答案.
详解:(1)如图1,延长EB交DG于点H,
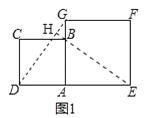
∵ABCD和AEFG为正方形,
∴在Rt△ADG和Rt△ABE中,
 ,
,
∴Rt△ADG≌Rt△ABE,
∴∠AGD=∠AEB,
∵∠HBG=∠EBA,
∴∠HGB+∠HBG=90°,
∴DG⊥BE;
(2)如图2,过点A作AP⊥BD交BD于点P,
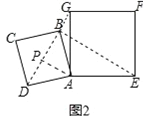
∵ABCD和AEFG为正方形,
∴在△DAG和△BAE中,
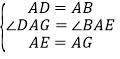 ,
,
∴△DAG≌△BAE(SAS),
∴DG=BE,
∵AD=2∠PDA=45°,∠APD=90°,
∴AP=DP=![]() ,
,
∵AG=2![]() ,∴PG=
,∴PG=![]() =
=![]() ,
,
∴DG=DP+PG=![]() +
+![]() ,
,
∵DG=BE,∴BE=![]() +
+![]() .
.


 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案科目:初中数学 来源: 题型:
【题目】用锤子以均匀的力敲击铁钉入木板.随着铁钉的深入,铁钉所受的阻力会越来越大,使得每次钉入木板的钉子的长度后一次为前一次的k倍(0<k<1).已知一个钉子受击3次后恰好全部进入木板,且第一次受击后进入木板部分的铁钉长度是钉长的 ![]() .设铁钉的长度为1,那么符合这一事实的方程是( )
.设铁钉的长度为1,那么符合这一事实的方程是( )
A.![]()
(1+k)2=1
B.![]()
k+ ![]() k2=1
k2=1
C.![]()
+ ![]() k+
k+ ![]() k2=1
k2=1
D.![]()
+ ![]() (1+k)2=1
(1+k)2=1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】城区某中学为形成体育特色,落实学生每天![]() 小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
小时的锻炼时间,通过调查研究,决定在七、八、九年级分别开展跳绳、羽毛球、毽球的健身运动.
国家规定初中每班的标准人数为![]() 人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的
人,七年级共有八个班,各班人数情况如下表,八年级学生人数是七年级学生人数的![]() 倍少
倍少![]() 人,九年级学生人数的
人,九年级学生人数的![]() 倍刚好是七、八年级学生人数的总和.(注:
倍刚好是七、八年级学生人数的总和.(注:![]() 班表示七年级一班)
班表示七年级一班)
班级 |
|
|
|
|
|
|
|
|
和每班标准 人数的差值 |
|
|
|
|
|
|
|
|
![]() 用含
用含![]() 的式子表示该中学七年级学生总数;
的式子表示该中学七年级学生总数;
![]() 学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根
学校决定按每人一根跳绳、一个毽球,两人一副羽毛球拍的标准,购买相应的体育器材以满足学生锻炼需要,其中跳绳每根![]() 元,毽球每个
元,毽球每个![]() 元,羽毛球拍每副
元,羽毛球拍每副![]() 元.请你计算当
元.请你计算当![]() 时,学校为落实
时,学校为落实![]() 小时体育锻炼时间需购买器材的费用是多少?
小时体育锻炼时间需购买器材的费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】根据题意,解答问题:
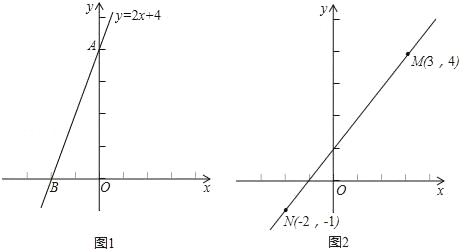
(1)如图1,已知直线y=2x+4与x轴、y轴分别交于A、B两点,求线段AB的长.
(2)如图2,类比(1)的解题过程,请你通过构造直角三角形的方法,求出点M(3,4)与点N(﹣2,﹣1)之间的距离.
(3)在(2)的基础上,若有一点D在x轴上运动,当满足DM=DN时,请求出此时点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
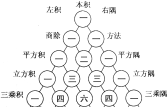
【题目】贾宪三角(如图)最初于11世纪被发现,原图(图2左)载于我国北宋时期数学家贾宪的著作中.这一成果比国外领先600年!这个三角形的构造法则是:两腰都是1,其余每个数为其上方左右两数之和.它给出(a+b)n(n为正整数)展开式(按a的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1,2,1,恰好对应着![]() 的展开式中的系数;第四行的四个数1,3,3,1,恰好对应着
的展开式中的系数;第四行的四个数1,3,3,1,恰好对应着![]() 展开式中的系数;等等.
展开式中的系数;等等.

(1)请根据贾宪三角直接写出![]() 的展开式:
的展开式:
![]() .
.
![]() .
.
(2)请用多项式乘法或所学的乘法公式验证你写出的![]() 的结果.
的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE. 
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某人用![]() 元购买了
元购买了![]() 套儿童服装,准备以一定价格出售,如果以每套儿童服装
套儿童服装,准备以一定价格出售,如果以每套儿童服装![]() 元的价格为标准,超出的记作正数,不足的记作负数,记录如下:
元的价格为标准,超出的记作正数,不足的记作负数,记录如下:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (单位:元)
(单位:元)
请你帮他计算出当他卖完这八套儿童服装后,赚了还是赔了,赚(或赔)了多少钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com