
【题目】如图,在ABCD中,E是AD上一点,延长CE到点F,使∠FBC=∠DCE. 
(1)求证:∠D=∠F;
(2)用直尺和圆规在AD上作出一点P,使△BPC∽△CDP(保留作图的痕迹,不写作法).
【答案】
(1)证明:BF交AD于G,如图,
∵四边形ABCD为平行四边形,
∴AD∥BC,
∴∠FBC=∠FGE,
而∠FBC=∠DCE,
∴∠FGE=∠DCE,
∵∠GEF=∠DEC,
∴∠D=∠F
(2)解:如图,点P为所作.

【解析】(1)BF交AD于G,先利用AD∥BC得到∠FBC=∠FGE,加上∠FBC=∠DCE,所以∠FGE=∠DCE,然后根据三角形内角和定理易得∠D=∠F;(2)分别作BC和BF的垂直平分线,它们相交于点O,然后以O为圆心,OC为半径作△BCF的外接圆⊙O,⊙O交AD于P,连结BP、CP,则根据圆周角定理得到∠F=∠BPC,而∠F=∠D,所以∠D=∠BPC,接着可证明∠PCD=∠APB=∠PBC,于是可判断△BPC∽△CDP.


科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为-7,点B表示的数为5,点C到点A,点B的距离相等,动点P从点A出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动的时间为![]() (
(![]() >0)秒
>0)秒
(1)点C表示的数是_________.
(2)求当![]() 等于多少秒时,点P到达点B处.
等于多少秒时,点P到达点B处.
(3)点P表示的数是_________(用含有![]() 的代数式表示).
的代数式表示).
(4)求当t等于多少秒时,PC之间的距离为2个单位长度(只列式,不计算).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,二次函数y=ax2+2ax﹣3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l: ![]() 对称.
对称. 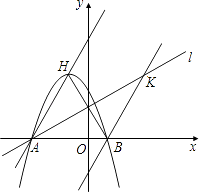
(1)求A、B两点坐标,并证明点A在直线l上;
(2)求二次函数解析式; 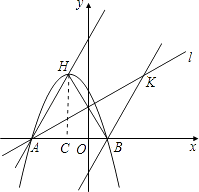
(3)过点B作直线BK∥AH交直线l于K点,M、N分别为直线AH和直线l上的两个动点,连接HN、NM、MK,求HN+NM+MK和的最小值. 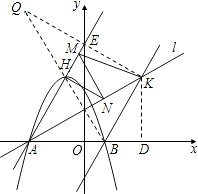
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明去文具用品商店给同学买某品牌水性笔,已知甲、乙两商店都有该品牌的水性笔且标价都是2元/支,但甲、乙两商店的优惠条件却不同.
甲商店:若购买不超过10支,则按标价付款;若一次购10支以上,则超过10支的部分按标价的60%付款. 乙商店:按标价的80%付款.
在水性笔的质量等因素相同的条件下.
(1)设小明要购买的该品牌笔数是x(x>10)支,请用含x的式子分别表示在甲、乙两个商店购买该品牌笔买水性笔的费用.
(2)若小明要购买该品牌笔30支,你认为在甲、乙两商店中,到哪个商店购买比较省钱?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
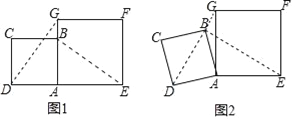
【题目】在数学兴趣小组活动中,小明进行数学探究活动,将边长为![]() 的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
的正方形ABCD与边长为2的正方形AEFG按图1位置放置,AD与AE在同一直线上,AB与AG在同一直线上.
(1)小明发现DG⊥BE,请你帮他说明理由;
(2)如图2,小明将正方形ABCD绕点A逆时针旋转,当点B恰好落在线段DG上时,请你帮他求出此时BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个水桶中装有少量且重量相等的水,先把甲桶的水倒出三分之一给乙桶,再把乙桶的水倒出四分之一给甲桶(假设不会溢出),最后甲、乙两桶中水的重量的大小是( )
A. 甲桶中水的重量>乙桶中水的重量 B. 甲桶中水的重量=乙桶中水的重量
C. 甲桶中水的重量<乙桶中水的重量 D. 不能确定,与桶中原有水的重量有关
查看答案和解析>>
科目:初中数学 来源: 题型:
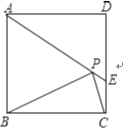
【题目】如图,在正方形ABCD中,AD=![]() ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
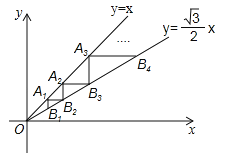
【题目】(2017辽宁省盘锦市,第18题,3分)如图,点A1(1,1)在直线y=x上,过点A1分别作y轴、x轴的平行线交直线![]() 于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线
于点B1,B2,过点B2作y轴的平行线交直线y=x于点A2,过点A2作x轴的平行线交直线![]() 于点B3,…,按照此规律进行下去,则点An的横坐标为______.
于点B3,…,按照此规律进行下去,则点An的横坐标为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com