
【题目】人们在长期的数学实践中总结了许多解决数学问题的方法,形成了许多光辉的数学想法,其中转化思想是中学教学中最活跃,最实用,也是最重要的数学思想,例如将不规则图形转化为规则图形就是研究图形问题比较常用的一种方法.
问题提出:求边长分别为、![]() 、
、![]() 、
、![]() 的三角形面积.
的三角形面积.
问题解决:
在解答这个问题时,先建立一个正方形网格(每个小正方形的边长为1),再在网格中画出边长分别为
![]() 、
、![]() 、
、![]() 的格点三角形
的格点三角形![]() (如图),
(如图),![]() 是角边为1和2的直角三角形斜边,
是角边为1和2的直角三角形斜边,![]() 是直角边分别为1和3的直角三角形的斜边,
是直角边分别为1和3的直角三角形的斜边,![]() 是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求
是直角边分别为2和3的直角三角形斜边,用一个大长方形的面积减去三个直角三角形的面积,这样不需求![]() 的高,而借用网格就能计算它的面积.
的高,而借用网格就能计算它的面积.
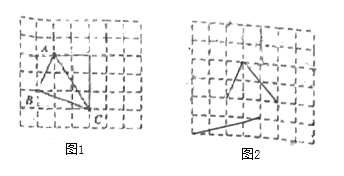
(1)请直接写出图①中![]() 的面积为____________.
的面积为____________.
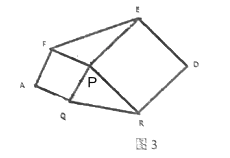
(2)类比迁移:求边长分别为![]() 、
、![]() 、
、![]() 的三角形面积(请利用图②的正方形网格画出相应的
的三角形面积(请利用图②的正方形网格画出相应的![]() ,并求出它的面积)
,并求出它的面积)
(3)思维拓展:求边长分别为![]() ,的三角形的面积
,的三角形的面积
(4)如图(3),已知![]() ,以
,以![]() ,
,![]() 为边向外作正方形
为边向外作正方形![]() ,正方形
,正方形![]() ,连接
,连接![]() ,若
,若![]() ,则六边形
,则六边形 ![]() 的面积是_________.
的面积是_________.
【答案】(1)![]() ;(2)3;(3)5ab;(4)31
;(2)3;(3)5ab;(4)31
【解析】
(1)直接利用△ABC所在矩形面积减去周围三角形面积进而得出答案;
(2)利用勾股定理结合矩形面积减去周围三角形面积进而得出答案;.
(3)结合(1)(2)易得此三角形的三边分别是直角边长为a,4b的直角三角形的斜边;直角边长为3a,2b的直角三角形的斜边;直角边长为2a,2b的直角三角形的斜边.用所在矩形减去周围三角形面积进而得出答案;
(4)将图3的六边形放入网格图中,即可发现其在9×5矩形内,用矩形面积减去周边四个直角三角形和一个梯形面积即可得到答案.
解:(1)S△ABC=3×3-![]() ×1×2-
×1×2-![]() ×1×3-
×1×3-![]() ×2×3=
×2×3=![]() ;
;
故答案为![]()
(2) 如图2所示:△ABC即为所求
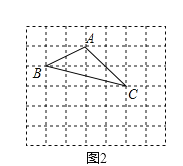
![]()
=![]()
=![]()
故答案为3
(3)如图为边长分别为![]() 的三角形,
的三角形,
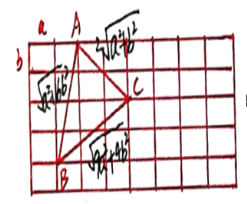
![]()
=![]()
=![]()
(4)如图所示,将六边形放入网格中,可见其在![]() 的矩形内,用矩形面积减去周边四个直角三角形和一个梯形的面积可得六边形的面积
的矩形内,用矩形面积减去周边四个直角三角形和一个梯形的面积可得六边形的面积

![]()
=![]()
=![]()


 寒假学与练系列答案
寒假学与练系列答案科目:初中数学 来源: 题型:
【题目】英国曼彻斯特大学物理学家安德烈·盖姆和康斯坦丁·诺沃肖洛夫,用微机械剥离法成功从石墨中分离出石墨烯,荣获了诺贝尔物理学奖.石墨烯具有优异的光学、电学、 力学特性,在材料学、微纳加工、能源、生物医学和药物传递等方面具有重要的应用前景,被认为是一种未来革命性的材料. 其理论厚度仅 0.000 000 000 34 m,将这个数据用科学记数法表示为_______m.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在平面直角坐标系内一直线l1:y=-x+3分别与x轴、y轴交于A、B两点,抛物线y=-x2+bx+c经过A、B两点,y轴右侧部分抛物线上有一动点C,过点C作y轴的平行线交直线l1于点D.
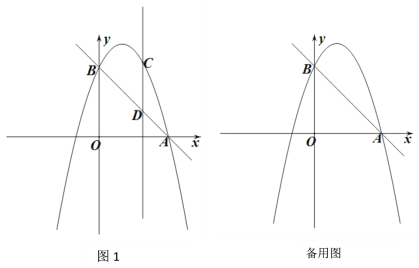
(1)求抛物线的函数表达式;
(2)如图1,C在第一象限,求以CD为直径的⊙E的最大面积,并判断此时⊙E与抛物线的对称轴是否相切?若不相切,求出使得⊙E与该抛物线对称轴相切时点C的横坐标;
(3)坐标平面内是否存在点M,使B、C、D、M为顶点的四边形为菱形?若存在,直接写出点M的坐标;不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
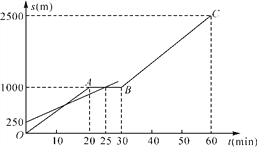
【题目】小明和爸爸从家步行去公园,爸爸先出发一直匀速前行,小明后出发.家到公园的距离为2500 m,如图是小明和爸爸所走的路程s(m)与步行时间t(min)的函数图象.
(1)直接写出小明所走路程s与时间t的函数关系式;
(2)小明出发多少时间与爸爸第三次相遇?
(3)在速度都不变的情况下,小明希望比爸爸早20 min到达公园,则小明在步行过程中停留的时间需作怎样的调整?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分10分)如图,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() (
(![]() 为常数,且
为常数,且![]() )的图象交于A(1,a)、B两点.
)的图象交于A(1,a)、B两点.
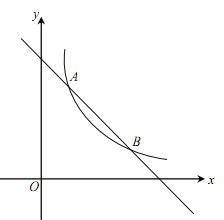
(1)求反比例函数的表达式及点B的坐标;
(2)在x轴上找一点P,使PA+PB的值最小,求满足条件的点P的坐标及△PAB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
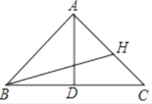
【题目】如图,在△ABC中,AB=10,BC=12,BC边上的中线AD=8.
(1)证明:△ABC为等腰三角形;
(2)点H在线段AC上,试求AH+BH+CH的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知反比例函数![]() 与一次函数y=kx+b的图象都经过点(-2,-1),且当x=3时这两个函数值相等.
与一次函数y=kx+b的图象都经过点(-2,-1),且当x=3时这两个函数值相等.
(1)求这两个函数的解析式;
(2)直接写出当x取何值时,![]() 成立.
成立.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组: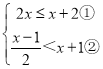
请结合题意填空,完成本题解答:
(1)解不等式①,得______;
(2)解不等式②,得______;
(3)把不等式①和②的解集在数轴上表示出来;
![]()
(4)原不等式组的解集为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com