
【题目】如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
(1)求证:BE=CF;
(2)当四边形ACDE为平行四边形时,求证:△ABE为等腰直角三角形.
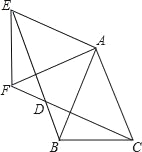
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)旋转的性质得AE=AB,AF=AC,∠EAF=∠BAC,则∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,利用AB=AC可得AE=AF,于是根据旋转的定义,△AEB可由△AFC绕点A按顺时针方向旋转得到,然后根据旋转的性质得到BE=CF;
(2) 首先证得△AFC为等腰直角三角形,然后即可证得△ABE为等腰直角三角形.
证明: (1)∵△AEF是由△ABC绕点A按顺时针方向旋转得到的,
∴AE=AB,AF=AC,∠EAF=∠BAC,
∴∠EAF+∠BAF=∠BAC+∠BAF,即∠EAB=∠FAC,
∵AB=AC,
∴AE=AF,
∴△AEB可由△AFC绕点A按顺时针方向旋转得到,
∴BE=CF;
(2)在□ABCD中,∠EAC+∠ACF=180°,
∴∠EAF=∠BAC=45°,
∴∠FAB+∠ACF=90°,
又AF=AC,
∴∠F=∠ACF,
∴∠FAB+∠F=90°,
∴∠ACF=45°,
∴△AFC为等腰直角三角形,
∴△ABE为等腰直角三角形.
故答案为:(1)证明见解析;(2)证明见解析.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
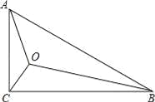
【题目】如图,在Rt△ABC中,∠C=90°,AC=1,BC=![]() ,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),则∠A′BC=______,OA+OB+OC=______.
,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),则∠A′BC=______,OA+OB+OC=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某古城几个地名的平面示意图,已知民俗街和博物馆的坐标分别为点![]() ,
,![]() ,请仔细观察示意图完成以下问题.
,请仔细观察示意图完成以下问题.

(1)请根据题意在图上建立平面直角坐标系.
(2)在(1)的条件下,写出图上B,D两地点的坐标.
(3)某周末甲,乙,丙,丁等4位同学分别到古城楼,民俗街,文化广场,博物馆四个地点游玩,且每人只去一个地点,老师打电话问了赵,钱,孙,李等四位同学,赵说:“甲在民俗街,乙在文化广场”;钱说:“丙在博物馆,乙在民俗街”;孙说:“丁在民俗街,丙在文化广场”;李说:“丁在古城楼,乙在文化广场”.若知道赵,钱,孙,李每人都只说对了一半,则丙同学游玩的地点是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD为正方形,点E为线段AC上一点,连接DE,过点E作EF⊥DE,交射线BC于点F,以DE、EF为邻边作矩形DEFG,连接CG.
(1)如图1,求证:矩形DEFG是正方形;
(2)若AB=2,CE=![]() ,求CG的长度;
,求CG的长度;
(3)当线段DE与正方形ABCD的某条边的夹角是30°时,直接写出∠EFC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图,有下列6个结论:
①abc<0;
②b<a﹣c;
③4a+2b+c>0;
④2c<3b;
⑤a+b<m(am+b),(m≠1的实数)
⑥2a+b+c>0,其中正确的结论的有_____.
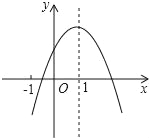
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,已知点A(a,a),B(a,a﹣3),其中a为整数.点C在线段AB上,且点C的横纵坐标均为整数.
(1)当a=1时,画出线段AB;
(2)若点C在x轴上,求出点C的坐标;
(3)若点C纵坐标满足![]() ,直接写出a的所有可能取值: .
,直接写出a的所有可能取值: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=AC,∠C=70°,△AB′C′与△ABC 关于直线 EF对称,∠CAF=10°,连接 BB′,则∠ABB′的度数是( )

A. 30° B. 35° C. 40° D. 45°
查看答案和解析>>
科目:初中数学 来源: 题型:
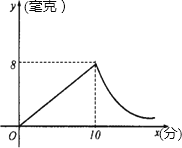
【题目】为预防“手足口病”,某校对教室进行“药熏消毒”.已知药物燃烧阶段,室内每立方米空气中的含药量y(毫克)与燃烧时间x(分钟)成正比例;燃烧阶段后,y与x成反比例(这两个变量之间的关系如图所示).现测得药物10分钟燃完,此时教室内每立方米空气含药量为8毫克.据以上信息解答下列问题:
(1)求药物燃烧时y与x的函数解析式.
(2)求药物燃烧阶段后y与x的函数解析式.
(3)当“药熏消毒”时间到50分钟时,每立方米空气中的含药量对人体方能无毒害作用,那么当“药熏消毒”时间到50分钟时每立方米空气中的含药量为多少毫克?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com