
【题目】下面是某古城几个地名的平面示意图,已知民俗街和博物馆的坐标分别为点![]() ,
,![]() ,请仔细观察示意图完成以下问题.
,请仔细观察示意图完成以下问题.

(1)请根据题意在图上建立平面直角坐标系.
(2)在(1)的条件下,写出图上B,D两地点的坐标.
(3)某周末甲,乙,丙,丁等4位同学分别到古城楼,民俗街,文化广场,博物馆四个地点游玩,且每人只去一个地点,老师打电话问了赵,钱,孙,李等四位同学,赵说:“甲在民俗街,乙在文化广场”;钱说:“丙在博物馆,乙在民俗街”;孙说:“丁在民俗街,丙在文化广场”;李说:“丁在古城楼,乙在文化广场”.若知道赵,钱,孙,李每人都只说对了一半,则丙同学游玩的地点是 .
【答案】(1)详见解析;(2)B(0,4) , D(-1,-1) ;(3)博物馆
【解析】
(1)根据点C或E点可确定原点的位置,然后建立直角坐标系即可;
(2)根据建立的直角坐标系即可直接写出B,D的坐标;
(3)先假设赵说的前半句是对的,然后发现与后面的话相矛盾,则说明赵说的后半句话是对的,然后按照每个人都对半句进行一一推理即可.
(1)根据点C的坐标可确定A点即为坐标原点,以此建立直角坐标系如下:
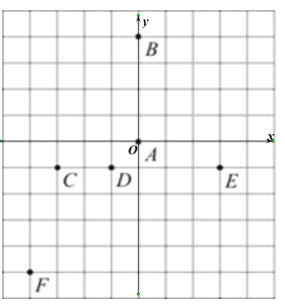
(2)根据平面直角坐标系,可知B(0,4) , D(-1,-1)
(3)假设赵说的前半句话“甲在民俗街”对,则钱说的前半句“丙在博物馆”就对,然后孙说的“丁在民俗街”就对,跟“甲在民俗街”矛盾,故赵说的前半句不对;
所以赵说的“乙在文化广场”对,则钱说的前半句“丙在博物馆”就对,则孙说的“丁在民俗街”就对,最后李说的“乙在文化广场”这半句是对的
综上所述,甲在古城楼,乙在文化广场,丙在博物馆,丁在民俗街.


科目:初中数学 来源: 题型:
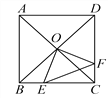
【题目】如图,正方形ABCD中,AB=8cm,对角线AC、BD相交于点O,点E、F分别从B、C两点同时出发,以1cm/s的速度沿BC、CD运动,到点C、D时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
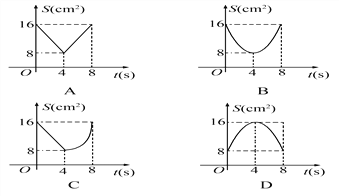
A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
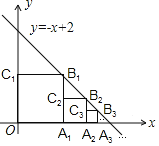
【题目】正方形![]() 、
、![]() 、
、![]() …按如图放置,其中点
…按如图放置,其中点![]() 、
、![]() 、
、![]() …在
…在![]() 轴正半轴上,点
轴正半轴上,点![]() 、
、![]() 、
、![]() …在直线
…在直线![]() 上,依此类推…,则点
上,依此类推…,则点![]() 的坐标是________;点
的坐标是________;点![]() 的坐标是_________.
的坐标是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1),Q (x2,y2)的对称中心的坐标为![]() ,如图.
,如图.
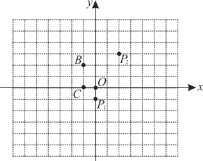
(1)在平面直角坐标系中,若点P1(0,-1),P2(2,3)的对称中心是点A,则点A的坐标为________;
(2)另取两点![]() ,
,![]() .有一电子青蛙从点P1处开始依次作关于点A,B,C的循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…,则点
.有一电子青蛙从点P1处开始依次作关于点A,B,C的循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
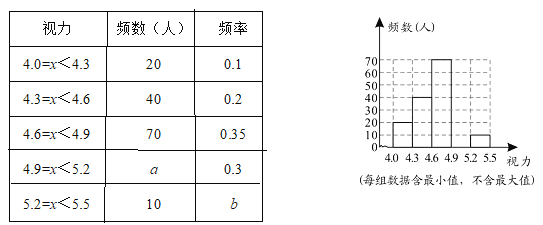
【题目】某校为了解八年级学生的视力情况,对八年级学生进行了一次视力调查,并将调查结果进行统计整理,绘制了频数分布表和频数分布直方图的一部分.
(1)在频数分布表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若将视力在4.6及以上的视力情况定义为“视力正常”,求“视力正常”的人数占被调查人数的百分比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面关于x的方程中:①ax2+x+2=0;②3(x﹣9)2﹣(x+1)2=1;③x+3=![]() ;④(a2+a+1)x2﹣a=0;⑤
;④(a2+a+1)x2﹣a=0;⑤![]() =x﹣1.一元二次方程的个数是( )
=x﹣1.一元二次方程的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,∠1=∠2,则不一定能使△ABD≌△ACD的条件是 ( )

A. AB=AC B. BD=CD C. ∠B=∠C D. ∠BDA=∠CDA
查看答案和解析>>
科目:初中数学 来源: 题型:
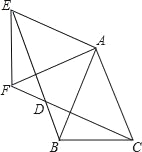
【题目】如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
(1)求证:BE=CF;
(2)当四边形ACDE为平行四边形时,求证:△ABE为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=﹣x2+2x.
(1)在给定的平面直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当y<0时,x的取值范围;
(3)若将此图象沿x轴向左平移3个单位,再沿y轴向下平移1个单位,请直接写出平移后图象所对应的函数关系式.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com