
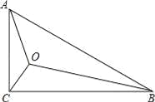
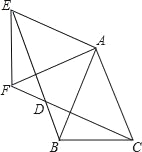
【题目】如图,在Rt△ABC中,∠C=90°,AC=1,BC=![]() ,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),则∠A′BC=______,OA+OB+OC=______.
,点O为Rt△ABC内一点,连接A0、BO、CO,且∠AOC=∠COB=BOA=120°,按下列要求画图(保留画图痕迹):以点B为旋转中心,将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),则∠A′BC=______,OA+OB+OC=______.
【答案】90° ![]() .
.
【解析】
(1)先根据三角函数的定义求出∠ABC的度数,再根据旋转的性质得OA=O′A′,BO=BO′,BA′=BA=2,∠OBO′=∠ABA′=60°,∠BO′A′=∠BOA=120°,则∠CBA′=∠CBA+∠ABA′=90°;
(2)先判断△BOO′为等边三角形,所以OO′=BO,∠BOO′=∠BO′O=60°,再证明点C、O、O′、A′共线,从而得到A′C=OC+OB+OA,然后利用勾股定理计算A′C即可.
解:(1)∵∠C=90°,AC=1,BC=![]() ,
,
∴tan∠ABC=![]() =
=![]() ,AB=2,
,AB=2,
∴∠ABC=30°,
∵将△AOB绕点B顺时针方向旋转60°,得到△A′O′B(得到A、O的对应点分别为点A′、O′),
∴OA=O′A′,BO=BO′,BA′=BA=2,∠OBO′=∠ABA′=60°,∠BO′A′=∠BOA=120°,
∴∠A′BC=∠CBA+∠ABA′=30°+60°=90°;
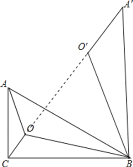
(2)∵BO=BO′,∠OBO′=∠ABA′=60°
∴△BOO′为等边三角形,
∴OO′=BO,∠BOO′=∠BO′O=60°,
而∠BOC=120°,
∴∠COO′=∠BOC+∠BOO′=60°+120°=180°,
∴点O′在直线CO上,
同理可得点O、O′、A′共线,
∴A′C=OC+OO′+O′A′=OC+OB+OA,
∵∠CBA′=∠CBA+∠ABA′=30°+60°=90°,
∴A′C=![]() =
=![]() ,
,
即OA+OB+OC=![]() .
.
故答案为90°,![]() .
.


科目:初中数学 来源: 题型:
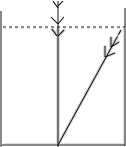
【题目】我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
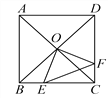
【题目】如图,正方形ABCD中,AB=8cm,对角线AC、BD相交于点O,点E、F分别从B、C两点同时出发,以1cm/s的速度沿BC、CD运动,到点C、D时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
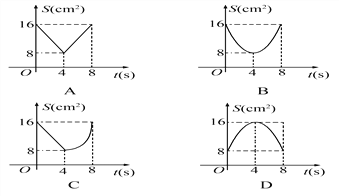
A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在我国古代数学著作《九章算术》中记载了这样一个问题:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”用现代语言表述为:如图,AB为⊙O的直径,弦CD⊥AB于点E,AE = 1寸,CD = 10寸,求直径AB的长.请你解答这个问题.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AD既是△ABC的中线,又是角平分线,请判断:
(1)△ABC的形状;
(2)AD是否过△ABC外接圆的圆心O,⊙O是否是△ABC的外接圆,并证明你的结论.
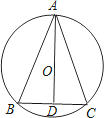
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 、
、![]() 、
、![]() …按如图放置,其中点
…按如图放置,其中点![]() 、
、![]() 、
、![]() …在
…在![]() 轴正半轴上,点
轴正半轴上,点![]() 、
、![]() 、
、![]() …在直线
…在直线![]() 上,依此类推…,则点
上,依此类推…,则点![]() 的坐标是________;点
的坐标是________;点![]() 的坐标是_________.
的坐标是_________.
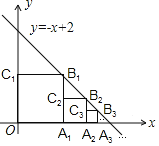
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】任意两点关于它们所连线段的中点成中心对称,在平面直角坐标系中,任意两点P(x1,y1),Q (x2,y2)的对称中心的坐标为![]() ,如图.
,如图.
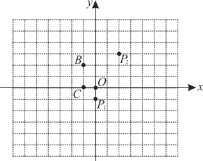
(1)在平面直角坐标系中,若点P1(0,-1),P2(2,3)的对称中心是点A,则点A的坐标为________;
(2)另取两点![]() ,
,![]() .有一电子青蛙从点P1处开始依次作关于点A,B,C的循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…,则点
.有一电子青蛙从点P1处开始依次作关于点A,B,C的循环对称跳动,即第一次跳到点P1关于点A的对称点P2处,接着跳到点P2关于点B的对称点P3处,第三次再跳到点P3关于点C的对称点P4处,第四次再跳到点P4关于点A的对称点P5处,…,则点![]() 的坐标为________.
的坐标为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=45°,△AEF是由△ABC绕点A按顺时针方向旋转得到的,连接BE、CF相交于点D
(1)求证:BE=CF;
(2)当四边形ACDE为平行四边形时,求证:△ABE为等腰直角三角形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com