
����Ŀ���ҹ��Ŵ���ѧ������������������������һ�����⣺���гط�һ�ɣ����������룬��ˮһ�ߣ����縰�������ڰ��룬��ˮ��糤�����Σ�����������˼��˵������һ���߳�Ϊ10�ߵ�������ˮ�أ���ˮ�ص������볤��һ��«έ��«έ¶��ˮ��1�ߣ�����«έ����ˮ��һ�ߵ��е㴦��«έ�Ķ���ǡ�õ���رߵ�ˮ�棬��ˮ����������«έ�ij��ȷֱ��Ƕ��٣�����ˮ�����Ϊx�ߣ�����Եõ�����_____��
���𰸡�x2+52����x+1��2��
��������
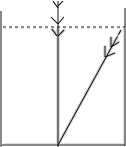
���ǿ��Խ���ת��Ϊ��ѧ����ͼ�Σ���ͼ��ʾ���������⣬��֪EB'�ij�Ϊ10�ߣ���B'C��5�ߣ����AB��AB'��x�ߣ���ʾ��ˮ��AC�����ݹ��ɶ����������̼��ɣ�
�����⻭��ͼ�Σ�
��«έ��AB��AB����x�ߣ���ˮ��AC����x��1���ߣ���ΪB'E��10�ߣ�����B'C��5�ߣ�
��Rt��AB'C����CB��2+AC2��AB��2
��52+��x��1��2��x2��
�ʴ�Ϊ��x2+52����x+1��2��


 ͨ��ѧ��Ĭд����ϵ�д�
ͨ��ѧ��Ĭд����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��AB�ǡ�O��ֱ������C�ڡ�O�ϣ�CD�ǡ�O�����ߣ�AD��CD�ڵ�D.E��AB�ӳ�����һ�㣬CE����O�ڵ�F������OC��AC.

(1)��֤��ACƽ�֡�DAO��
(2)����DAO=105������E=30��.�����OCE�Ķ���.������O�İ뾶Ϊ![]() �����߶�EF�ij�.
�����߶�EF�ij�.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ŵ�Ӱ�����˵�����ӳ���ƻô����������������ܵ�������Ե����������˵�����״���硷�����塷�������Ǽ�Ԫ���IJ�С˵��ij���������������֪�����˵������۵����롶��״���硷��ͬ�������塷�����۵����ǡ������Ǽ�Ԫ�����۵�3���������˵����롶�����Ǽ�Ԫ���ĵ��ۺʹ���40Ԫ�Ҳ�����50Ԫ�����Ե�Ӱ��ӳ�����������˵����롶�����Ǽ�Ԫ��������������ͬ������״���硷����������Ϊ�����塷����������3���������˵����롶���塷������������Ϊ450�����ҡ����˵����������������ڡ����塷����������![]() ��С��230���������˵������塷����������֮�ͱȡ���״���硷�������Ǽ�Ԫ���������۶�֮�Ͷ�1575Ԫ�������˵������塷��2��С˵������֮�����ʱ�������˵��ĵ���Ϊ_____Ԫ��
��С��230���������˵������塷����������֮�ͱȡ���״���硷�������Ǽ�Ԫ���������۶�֮�Ͷ�1575Ԫ�������˵������塷��2��С˵������֮�����ʱ�������˵��ĵ���Ϊ_____Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���ABC���������㶼�ڸ���ϣ���A������Ϊ��2��2�������������⣺
��1��������ABC����ԭ��O�����ĶԳƵ���A1B1C1����д��A1�����ꣻ
��2��������ABC�Ƶ�B��ʱ����ת90����õ�����A2B2C2���������C����ת�����о�����·�����Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��С���ⷽ��![]() =3�����˴����������£�
=3�����˴����������£�
�������߶�����(x-2)����1-(1-x)=3(��һ��)
ȥ���ţ���1-1+x=3(�ڶ���)
����ϲ�ͬ�����x=3(������)
���飬��x=3ʱx-2��0(���IJ�)
����x=3��ԭ���̵Ľ⣮(���岽)
(1)С���������Ǵӵ�____����ʼ�����ģ�ԭ���̻�Ϊ��һ���ĸ�����_____��
(2)��д��������ȷ�Ľ����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����Rt��ABC��Rt��DEF����ͼ1�ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB����EDF��90������DEF��45����AC��8cm��BC��6cm��EF��9cm����ͼ2����DEF��ͼ1��λ�ó�������1cm/s���ٶ���CB���ABC�����ƶ����ڡ�DEF�ƶ���ͬʱ����P�ӡ�ABC�Ķ���B��������2cm/s���ٶ���BA���A�����ƶ�������DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ�ƶ�����PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ�����ƶ�ʱ��Ϊt��s����0��t��4.5��������������⣺
��1���ú�t�Ĵ���ʽ��ʾ�߶�AP���� ����
��2����tΪ��ֵʱ����E�ڡ�A��ƽ�����ϣ�
��3����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��4������PE����t��1��s��ʱ�����ı���APEC�������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
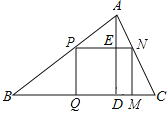
����Ŀ���α�����һ����ҵ�⣺
��һ������������ABC�����ı�BC=120mm����AD=80mm��Ҫ�����ӹ��������������ʹ�����ε�һ����BC�ϣ�������������ֱ���AB��AC�ϣ��ʼӹ��ɵ�����������ı߳��Ƕ���mm��
Сӱ��ô���Ĵ�Ϊ48mm��Сӱ���ڷ�˼��������������µ����⣮
��1�����ԭ����Ҫ�ӹ��������һ�����Σ��Ҵ˾��������������ŷ��õ�����������ɣ���ͼ1����ʱ�������������������߳��ֱַ�Ϊ����mm��������㣮
��2�����ԭ������Ҫ�ӹ������ֻ��һ�����Σ���ͼ2���������˾�������������߳��Ͳ���ȷ���������������������ֵ����ﵽ������ֵʱ��������������߳���
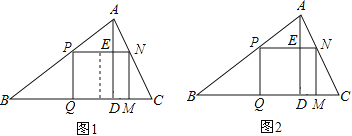
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���![]() ��ͼ�����ϣ�ͼ����
��ͼ�����ϣ�ͼ����![]() ��
��![]() ������
������![]() ���ཻ�ڸ�������
���ཻ�ڸ�������
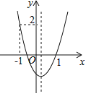
��![]() �ʣ������ĸ����ۣ���
�ʣ������ĸ����ۣ���![]() ����
����![]() ����
����![]() ����
����![]() ��д��������ȷ���۵���ţ���Ե�
��д��������ȷ���۵���ţ���Ե�![]() �֣���ѡ����ѡ�����÷֣�
�֣���ѡ����ѡ�����÷֣�
�� ![]() �ʣ������ĸ����ۣ���abc��0����2a+b��0����a+c=1����a��1��д��������ȷ���۵���ţ�
�ʣ������ĸ����ۣ���abc��0����2a+b��0����a+c=1����a��1��д��������ȷ���۵���ţ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C=90�㣬AC=1��BC=![]() ����OΪRt��ABC��һ�㣬����A0��BO��CO���ҡ�AOC=��COB=BOA=120�㣬������Ҫ��ͼ��������ͼ�ۼ������Ե�BΪ��ת���ģ�����AOB�Ƶ�B˳ʱ�뷽����ת60�㣬�õ���A��O��B���õ�A��O�Ķ�Ӧ��ֱ�Ϊ��A�䡢O�䣩�����A��BC=______��OA+OB+OC=______.
����OΪRt��ABC��һ�㣬����A0��BO��CO���ҡ�AOC=��COB=BOA=120�㣬������Ҫ��ͼ��������ͼ�ۼ������Ե�BΪ��ת���ģ�����AOB�Ƶ�B˳ʱ�뷽����ת60�㣬�õ���A��O��B���õ�A��O�Ķ�Ӧ��ֱ�Ϊ��A�䡢O�䣩�����A��BC=______��OA+OB+OC=______.
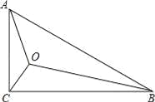
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com