
【题目】课本中有一道作业题:
有一块三角形余料ABC,它的边BC=120mm,高AD=80mm.要把它加工成正方形零件,使正方形的一边在BC上,其余两个顶点分别在AB,AC上.问加工成的正方形零件的边长是多少mm?
小颖解得此题的答案为48mm,小颖善于反思,她又提出了如下的问题.
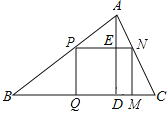
(1)如果原题中要加工的零件是一个矩形,且此矩形是由两个并排放置的正方形所组成,如图1,此时,这个矩形零件的两条边长又分别为多少mm?请你计算.
(2)如果原题中所要加工的零件只是一个矩形,如图2,这样,此矩形零件的两条边长就不能确定,但这个矩形面积有最大值,求达到这个最大值时矩形零件的两条边长.
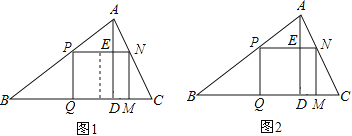
【答案】(1)![]() mm,
mm,![]() mm;(2)PN=60mm,
mm;(2)PN=60mm,![]() mm.
mm.
【解析】
试题(1)、设PQ=y(mm),则PN=2y(mm),AE=80-y(mm),根据平行得出△APN和△ABC相似,根据线段的比值得出y的值,然后得出边长;(2)、根据第一题同样的方法得出y与x的函数关系式,然后求出S与x的函数关系式,根据二次函数的性质得出最大值.
试题解析:(1)、设PQ=y(mm),则PN=2y(mm),AE=80-y(mm)
∵PN∥BC, ∴![]() =
=![]() ,△APN∽△ABC ∴
,△APN∽△ABC ∴![]() =
=![]() ∴
∴![]() =
=![]()
∴![]() =
=![]() 解得 y=
解得 y=![]() ∴2y=
∴2y=![]()
∴这个矩形零件的两条边长分别为![]() mm,
mm,![]() mm
mm
(2)、设PQ=x(mm),PN=y(mm),矩形面积为S ,则AE=80-x(mm)。.
由(1)知![]() =
=![]() ∴
∴![]() =
=![]() ∴ y=
∴ y=![]()
则S=xy=![]() =
=![]() =
=![]()
∵![]() ∴ S有最大值 ∴当x=40时,S最大=2400(mm2) 此时,y=
∴ S有最大值 ∴当x=40时,S最大=2400(mm2) 此时,y=![]() ="60" 。
="60" 。
∴面积达到这个最大值时矩形零件的两边PQ、PN长分别是40 mm ,60 mm。


科目:初中数学 来源: 题型:
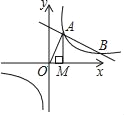
【题目】如图,一次函数y=﹣![]() x+
x+![]() 的图象与反比例函数y=
的图象与反比例函数y=![]() (k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.
(k>0)的图象交于A,B两点,过A点作x轴的垂线,垂足为M,△AOM面积为1.
(1)求反比例函数的解析式;
(2)在y轴上求一点P,使PA+PB的值最小,并求出其最小值和P点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点C、D在⊙O上,∠A=2∠BCD,点E在AB的延长线上,∠AED=∠ABC

(1)求证:DE与⊙O相切;
(2)若BF=2,DF=![]() ,求⊙O的半径.
,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
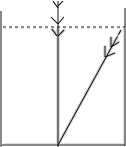
【题目】我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
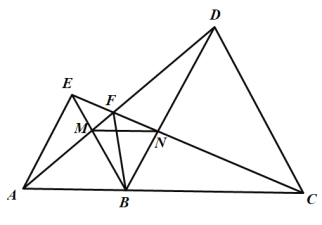
【题目】如图,![]() ,
,![]() 均为等边三角形,点
均为等边三角形,点![]() ,
,![]() ,
,![]() 在同一条直线上,连接
在同一条直线上,连接![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,连接
,连接![]() ,下列结论正确的有_________.
,下列结论正确的有_________.
①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;⑤
;⑤![]() 平分
平分![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
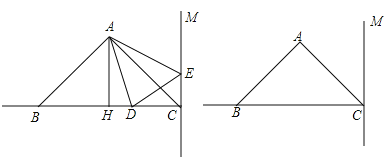
【题目】如图,在△ABC中,已知AB=AC,∠BAC=90°,AH是△ABC的高,AH=4 cm,BC=8 cm,直线CM⊥BC,动点D从点C开始沿射线CB方向以每秒3厘米的速度运动,动点E也同时从点C开始在直线CM上以每秒1厘米的速度向远离C点的方向运动,连接AD、AE,设运动时间为t(t>0)秒.
(1)请直接写出CD、CE的长度(用含有t的代数式表示):CD= cm,CE= cm;
(2)当t为多少时,△ABD的面积为12 cm2?
(3)请利用备用图探究,当t为多少时,△ABD≌△ACE?并简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD中,AB=8cm,对角线AC、BD相交于点O,点E、F分别从B、C两点同时出发,以1cm/s的速度沿BC、CD运动,到点C、D时停止运动,设运动时间为t(s),△OEF的面积为S(cm2),则S(cm2)与t(s)的函数关系可用图象表示为( )
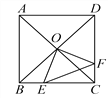
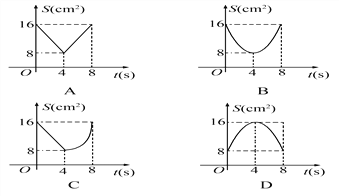
A. A B. B C. C D. D
查看答案和解析>>
科目:初中数学 来源: 题型:
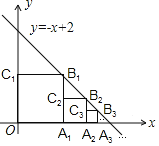
【题目】正方形![]() 、
、![]() 、
、![]() …按如图放置,其中点
…按如图放置,其中点![]() 、
、![]() 、
、![]() …在
…在![]() 轴正半轴上,点
轴正半轴上,点![]() 、
、![]() 、
、![]() …在直线
…在直线![]() 上,依此类推…,则点
上,依此类推…,则点![]() 的坐标是________;点
的坐标是________;点![]() 的坐标是_________.
的坐标是_________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com