
【题目】如图,在平面直角坐标系中,二次函数![]() 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.

(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形![]() .是否存在点P,使四边形
.是否存在点P,使四边形![]() 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
【答案】解:(1)将B、C两点的坐标代入![]() ,得
,得
![]() , 解得
, 解得![]() 。
。
∴二次函数的解析式为![]() 。
。
(2)存在。如图1,假设抛物线上存在点P,使四边形![]() 为菱形,连接
为菱形,连接![]() 交CO于点E。
交CO于点E。
∵四边形![]() 为菱形, K∴PC=PO,且PE⊥CO。
为菱形, K∴PC=PO,且PE⊥CO。
∴OE=EC=![]() ,即P点的纵坐标为
,即P点的纵坐标为![]() 。
。
由![]() 解得:
解得:
![]() (不合题意,舍去)。
(不合题意,舍去)。
∴存在这样的点,此时P点的坐标为(![]() ,
,![]() )。
)。
(3)如图2,连接PO,作PM⊥x于M,PN⊥y于N。设P点坐标为(x,![]() ),
),

由![]() =0,得点A坐标为(-1,0)。
=0,得点A坐标为(-1,0)。
∴AO=1,OC=3, OB=3,PM=![]() ,PN=x。
,PN=x。
∴S四边形ABPC=![]() +
+![]() +
+![]()
=![]() AO·OC+
AO·OC+![]() OB·PM+
OB·PM+![]() OC·PN
OC·PN
=![]() ×1×3+
×1×3+![]() ×3×(
×3×(![]() )+
)+![]() ×3×x
×3×x
=![]() =
=![]() 。
。
∴当x=![]() 时,四边形ABPC的面积最大.此时P点坐标为(
时,四边形ABPC的面积最大.此时P点坐标为(![]() ,
,![]() ),四边形ABPC的最大面积为
),四边形ABPC的最大面积为![]() 。
。
【解析】
试题(1)直接把B(3,0)、C(0,-3)代入![]() 可得到关于b、c的方程组,解方程组求得b,c,则从而求得二次函数的解析式。
可得到关于b、c的方程组,解方程组求得b,c,则从而求得二次函数的解析式。
(2)假设抛物线上存在点P,使四边形![]() 为菱形,连接
为菱形,连接![]() 交CO于点E,则PO=PC,根据翻折的性质得OP′=OP,CP′=CP,易得四边形POP′C为菱形,又E点坐标为(0,
交CO于点E,则PO=PC,根据翻折的性质得OP′=OP,CP′=CP,易得四边形POP′C为菱形,又E点坐标为(0,![]() ),则点P的纵坐标为
),则点P的纵坐标为![]() ,把y=
,把y=![]()
代入![]() 可求出对应x的值,然后确定满足条件的P点坐标。
可求出对应x的值,然后确定满足条件的P点坐标。
(3)由S四边形ABPC=![]() +
+![]() +
+![]() 求出S四边形ABPC关于P点横坐标的函数表达式,应用二次函数的最值原理求解。
求出S四边形ABPC关于P点横坐标的函数表达式,应用二次函数的最值原理求解。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,∠ACB=90°,AC=BC,BE⊥CE于E,AD⊥CE于D,BE=3cm,AD=9cm.
求:(1)DE的长;
(2)若CE在△ABC的外部(如图),其它条件不变,DE的长是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一张四边形纸片沿EF折叠,以下条件中能得出AD∥BC的条件个数是( )
①∠2=∠4:②∠2+∠3=180°;③∠1=∠6:④∠4=∠5

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】宁波至绍兴城际列车已于2019年7月10日运营,这是国内首条利用既有铁路改造开行的跨市域城际铁路.其中余姚至绍兴的成人票价12元/人,学生票价6元/人.余姚某校801班师生共计50人坐城际列车去绍兴秋游.
(1)设有![]() 名老师,求801班师生从余姚到绍兴的城际列车总费用
名老师,求801班师生从余姚到绍兴的城际列车总费用![]() 关于
关于![]() 的函数表达式.
的函数表达式.
(2)若从余姚到绍兴的城际列车总费用![]() 不超过330元,问至少有几名学生?
不超过330元,问至少有几名学生?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知∠MON及其边上一点A,以点A为圆心,AO长为半径画弧,分别交OM,ON于点B和C,再以点C为圆心,AC长为半径画弧,恰好经过点B,错误的结论是( ).
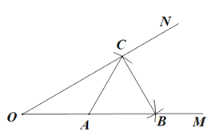
A.![]() B.∠OCB=90°C.∠MON=30°D.OC=2BC
B.∠OCB=90°C.∠MON=30°D.OC=2BC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知x2+(a+3)x+a+1=0是关于x的一元二次方程.
(1)求证:方程总有两个不相等的实数根;
(2)若方程的两个实数根为x1 ,x2 ,且x12+x22=10,求实数a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我国古代数学的许多创新与发展都曾居世界前列,其中“杨辉三角”(如图)就是一例,它的发现比欧洲早五百年左右.

杨辉三角两腰上的数都是1,其余每个数为它的上方(左右)两数之和.事实上,这个三角形给出了![]() (n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律. 例如,在三角形中第三行的三个数1,2,1,恰好对应着
(n=1,2,3,4,5,6)的展开式(按a的次数由大到小的顺序排列)的系数规律. 例如,在三角形中第三行的三个数1,2,1,恰好对应着![]() 展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着
展开式中各项的系数;第四行的四个数1,3,3,1,恰好对应着![]() 展开式中各项的系数,等等.
展开式中各项的系数,等等.
(1)当n=4时,![]() 的展开式中第3项的系数是_________;
的展开式中第3项的系数是_________;
(2)人们发现,当n是大于6的自然数时,这个规律依然成立,那么![]() 的展开式中各项的系数的和为_________.
的展开式中各项的系数的和为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点坐标是(2,﹣1),且经过点A(5,8)
(1)求该抛物线的解析式;
(2)设该抛物线与y轴相交于点B,与x轴相交于C、D两点(点C在点D的左边),试求点B、C、D的坐标;
(3)设点P是x轴任一点,连接AP、BP.试求当AP+BP取得最小值时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为8的正方形ABCD中,点O为AD上一动点(4<OA<8),以O为圆心,OA的长为半径的圆交边CD于点M,连接OM,过点M作⊙O的切线交边BC于N.
(1)求证:△ODM∽△MCN;
(2)设DM=x,求OA的长(用含x的代数式表示);
(3)在点O的运动过程中,设△CMN的周长为P,试用含x的代数式表示P,你能发现怎样的结论?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com